题目内容
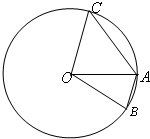（2012•宣城模拟）如图，⊙O的半径为1，点A，B，C是⊙O上的点，且∠AOB=30°，AC=2AB，则| OA |
| BC |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
分析：由⊙O的半径为1，点A，B，C是⊙O上的点，且∠AOB=30°，AC=2AB，知|
|2=12+12-2cos30°=2-
，|
|2=4|
|2=8-4
，由此能求出
•
的值．
| AB |
| 3 |
| AC |
| AB |
| 3 |
| OA |
| BC |
解答：解：如图，∵⊙O的半径为1，点A，B，C是⊙O上的点，且∠AOB=30°，AC=2AB，
∴|
|2=12+12-2cos30°=2-
，
|
|2=4|
|2=8-4
，
∴
•
=
•(
-
)
=
•
-
•
=
|
|2-
|
|2
=
-3．
故答案为：
-3．
∴|| AB |
| 3 |
|
| AC |
| AB |
| 3 |
∴
| OA |
| BC |
=
| OA |
| AC |
| AB |
=
| AO |
| AB |
| AO |
| AC |
=
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
=
| 3 |
| 2 |
| 3 |
故答案为：
| 3 |
| 2 |
| 3 |
点评：主要考查向量数量积等运算，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目