题目内容
已知函数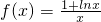
(1)若k>0且函数f(x)在区间(k,k+ )上存在极值,求实数k的取值范围
)上存在极值,求实数k的取值范围
(2)如果存在x∈[2,+∞),使得不等式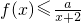 成立,求实数a的取值范围.
成立,求实数a的取值范围.
解:(1)∵函数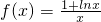 ,
,
∴ ,
,
由 ,得x=1,
,得x=1,
由条件 ,
,
解得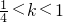 .
.
(2)∵
=(1+ )(1+lnx),
)(1+lnx),
设g(x)=(1+ )(1+lnx),
)(1+lnx),
 ,
,
再设h(x)=x-2lnx, ,
,
∴h(x)增,h(x)≥h(2)>0,
∴g′(x)>0,g(x)增.
∴g(x)≥g(2)=2(1+ln2),
∴a≥2+2ln2.
分析:(1)由 ,得x=1,再由
,得x=1,再由 ,能求出实数k的取值范围.
,能求出实数k的取值范围.
(2) =(1+
=(1+ )(1+lnx),设g(x)=(1+
)(1+lnx),设g(x)=(1+ )(1+lnx),则
)(1+lnx),则 ,再设h(x)=x-2lnx,则h(x)增,h(x)≥h(2)>0,坆g′(x)>0,g(x)增.由此能求出实数a的取值范围.
,再设h(x)=x-2lnx,则h(x)增,h(x)≥h(2)>0,坆g′(x)>0,g(x)增.由此能求出实数a的取值范围.
点评:本题考查利用导数求闭区间上函数的最值的应用,考查运算求解能力,考查论证推理能力,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
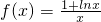 ,
,∴
 ,
,由
 ,得x=1,
,得x=1,由条件
 ,
,解得
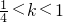 .
.(2)∵

=(1+
 )(1+lnx),
)(1+lnx),设g(x)=(1+
 )(1+lnx),
)(1+lnx), ,
,再设h(x)=x-2lnx,
 ,
,∴h(x)增,h(x)≥h(2)>0,
∴g′(x)>0,g(x)增.
∴g(x)≥g(2)=2(1+ln2),
∴a≥2+2ln2.
分析:(1)由
 ,得x=1,再由
,得x=1,再由 ,能求出实数k的取值范围.
,能求出实数k的取值范围.(2)
 =(1+
=(1+ )(1+lnx),设g(x)=(1+
)(1+lnx),设g(x)=(1+ )(1+lnx),则
)(1+lnx),则 ,再设h(x)=x-2lnx,则h(x)增,h(x)≥h(2)>0,坆g′(x)>0,g(x)增.由此能求出实数a的取值范围.
,再设h(x)=x-2lnx,则h(x)增,h(x)≥h(2)>0,坆g′(x)>0,g(x)增.由此能求出实数a的取值范围.点评:本题考查利用导数求闭区间上函数的最值的应用,考查运算求解能力,考查论证推理能力,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
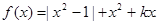
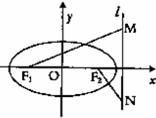
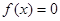 的解;
的解;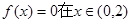 上有两个解
上有两个解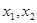 ,求k取值范围并证明
,求k取值范围并证明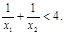
 (2)若关于x的方程
(2)若关于x的方程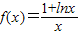
 )上存在极值,求实数k的取值范围
)上存在极值,求实数k的取值范围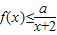 成立,求实数a的取值范围.
成立,求实数a的取值范围.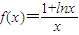
 )上存在极值,求实数k的取值范围
)上存在极值,求实数k的取值范围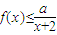 成立,求实数a的取值范围.
成立,求实数a的取值范围.