题目内容
已知函数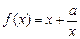 的定义域为
的定义域为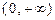 ,且
,且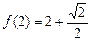 . 设点
. 设点 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点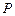 分别作直线
分别作直线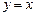 和
和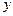 轴的垂线,垂足分别为
轴的垂线,垂足分别为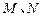 .
.
(1)求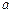 的值;
的值;
(2)问: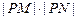 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设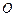 为坐标原点,求四边形
为坐标原点,求四边形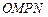 面积的最小值.
面积的最小值.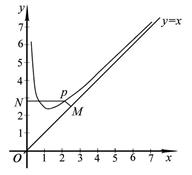
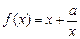 的定义域为
的定义域为 ,且
,且 . 设点
. 设点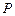 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点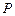 分别作直线
分别作直线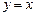 和
和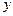 轴的垂线,垂足分别为
轴的垂线,垂足分别为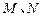 .
.(1)求
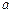 的值;
的值;(2)问:
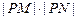 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;(3)设
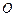 为坐标原点,求四边形
为坐标原点,求四边形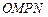 面积的最小值.
面积的最小值.
(1) .(2)有
.(2)有 ,即
,即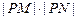 为定值,这个值为1.
为定值,这个值为1.
(3)四边形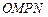 面积有最小值
面积有最小值 .
.
 .(2)有
.(2)有 ,即
,即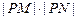 为定值,这个值为1.
为定值,这个值为1. (3)四边形
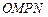 面积有最小值
面积有最小值 .
. (1)∵  ,∴
,∴  .
.
(2)设点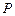 的坐标为
的坐标为 ,则有
,则有
 ,
, ,
,
由点到直线的距离公式可知: ,
,
故有 ,即
,即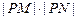 为定值,这个值为1.
为定值,这个值为1.
(3)由题意可设 ,可知
,可知 .
.
∵ 与直线
与直线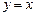 垂直,∴
垂直,∴  ,即
,即  ,
,
解得 ,又
,又 ,∴
,∴  .
.
∴ ,
,  ,
,
∴ ,
,
当且仅当 时,等号成立.
时,等号成立.
∴ 此时四边形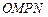 面积有最小值
面积有最小值 .
.
 ,∴
,∴  .
. (2)设点
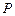 的坐标为
的坐标为 ,则有
,则有 ,
, ,
,
由点到直线的距离公式可知:
 ,
, 故有
 ,即
,即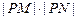 为定值,这个值为1.
为定值,这个值为1. (3)由题意可设
 ,可知
,可知 .
.∵
 与直线
与直线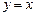 垂直,∴
垂直,∴  ,即
,即  ,
,解得
 ,又
,又 ,∴
,∴  .
.∴
 ,
,  ,
, ∴
 ,
, 当且仅当
 时,等号成立.
时,等号成立.∴ 此时四边形
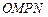 面积有最小值
面积有最小值 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=
,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=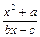 有且仅有两个不动点0和2.
有且仅有两个不动点0和2.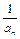 )=1,
)=1,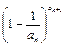 <
<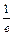 <
<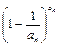 ;
;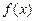 、
、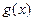 ,如果存在实数
,如果存在实数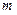 、
、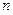 使得
使得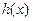 =
=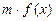 +
+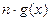 ,则称函数
,则称函数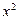 +
+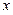 和
和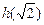 的值;
的值;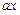 ,
,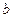
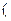
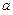 ,
,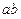 ≠0
≠0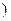 生成,求
生成,求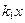 +
+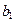 ,
,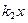 +
+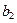
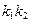 ≠0
≠0 ,已知实数x,y满足|x|≤2,|y|≤2,
,已知实数x,y满足|x|≤2,|y|≤2,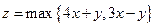 则z的取值范围是 ( )
则z的取值范围是 ( )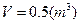 为定值时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小
为定值时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小 (参考数据:
(参考数据: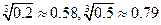 ,
,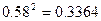 ,
,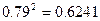 )
)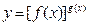 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得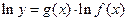 ,两边同时求导得
,两边同时求导得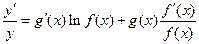 ,于是
,于是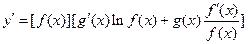 .运用此方法可以探求
.运用此方法可以探求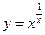 的一个单调递增区间是( )
的一个单调递增区间是( )
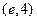
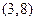
 满足对任意的
满足对任意的 都有
都有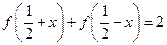 成立,则
成立,则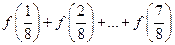 = .
= . ,例如:1
,例如:1 2=1,3
2=1,3 的值域为 .
的值域为 .