题目内容
求函数 的最小值,其中a>0.
的最小值,其中a>0.
解:由题意得,a>0,则函数的定义域为R,
 =
= ,
,
设t= ,则t
,则t ,函数变为y=
,函数变为y= ,且t
,且t ,
,
∴函数y= 在(0,1)上递减,在(1,+∞)上递增,
在(0,1)上递减,在(1,+∞)上递增,
当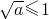 时,即0<a≤1时,函数的最小值为:ymin=1+1=2,
时,即0<a≤1时,函数的最小值为:ymin=1+1=2,
当 时,即a>1时,函数的最小值为:ymin=
时,即a>1时,函数的最小值为:ymin= ,
,
综上得,当0<a≤1时,ymin=2;当a>1时,ymin= .
.
分析:先由题意求出函数的定义域,再利用分离常数法将解析式化简,再进行换元并求出未知数的范围,代入后求出函数的单调性,再对a进行分类求出对应的最小值.
点评:本题考查了利用函数的单调性求最值问题,关键是利用分离常数法将解析式化简,考查了分离常数法和换元法,分类讨论思想.
 =
= ,
,设t=
 ,则t
,则t ,函数变为y=
,函数变为y= ,且t
,且t ,
,∴函数y=
 在(0,1)上递减,在(1,+∞)上递增,
在(0,1)上递减,在(1,+∞)上递增,当
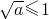 时,即0<a≤1时,函数的最小值为:ymin=1+1=2,
时,即0<a≤1时,函数的最小值为:ymin=1+1=2,当
 时,即a>1时,函数的最小值为:ymin=
时,即a>1时,函数的最小值为:ymin= ,
,综上得,当0<a≤1时,ymin=2;当a>1时,ymin=
 .
.分析:先由题意求出函数的定义域,再利用分离常数法将解析式化简,再进行换元并求出未知数的范围,代入后求出函数的单调性,再对a进行分类求出对应的最小值.
点评:本题考查了利用函数的单调性求最值问题,关键是利用分离常数法将解析式化简,考查了分离常数法和换元法,分类讨论思想.

练习册系列答案
相关题目
 :
: ,其中等于
,其中等于 的项有
的项有 个
个 ,
,
 ,
,
 .
. ,求
,求 ;
; ,求函数
,求函数 的最小值.
的最小值. 的最小值,其中
的最小值,其中
 :
: ,其中等于
,其中等于 的项有
的项有 个
个 ,
,
 ,
,
 .
. ,求
,求 ;
; ,求函数
,求函数 的最小值.
的最小值.