题目内容
(Ⅰ)已知函数:![]() 求函数
求函数![]() 的最小值;
的最小值;
(Ⅱ)证明:![]() ;
;
(Ⅲ)定理:若![]() 均为正数,则有
均为正数,则有![]() 成立(其中
成立(其中![]() .请你构造一个函数
.请你构造一个函数![]() ,证明:
,证明:
当![]() 均为正数时,
均为正数时,![]() .
.
(Ⅰ)当![]() 时,
时,![]() 的最小值为
的最小值为![]() (Ⅱ)证明见解析(Ⅲ)证明见解析
(Ⅱ)证明见解析(Ⅲ)证明见解析
解析:
(Ⅰ)令![]()
得![]() ……………………………………2分
……………………………………2分
当![]() 时,
时,![]()
![]() 故
故![]() 在
在![]() 上递减.
上递减.
当![]() 故
故![]() 在
在![]() 上递增.
上递增.
所以,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ….……………………………………..4分
….……………………………………..4分
(Ⅱ)由![]() ,有
,有![]() 即
即![]()
故 ![]() .………………………………………5分
.………………………………………5分
(Ⅲ)证明:要证: ![]()
只要证:![]()
设![]()
![]() …………………7分
…………………7分
则![]()
令![]() 得
得![]() …………………………………………………….8分
…………………………………………………….8分
当![]()
![]() 时,
时,![]()
![]()
![]()
故![]() 上递减,类似地可证
上递减,类似地可证![]() 递增
递增
所以![]() 的最小值为
的最小值为![]() ………………10分
………………10分
而![]() =
=![]()
=![]()
=![]()
由定理知: ![]() 故
故![]()
![]()
故![]()
即: ![]() .…………………………..14分
.…………………………..14分
………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 的最小正周期;
的最小正周期; 上的函数值的取值范围.
上的函数值的取值范围. .
. 的最小正周期;
的最小正周期; 上的函数值的取值范围.
上的函数值的取值范围. .
. 的最小正周期;
的最小正周期;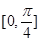 上的函数值的取值范围.
上的函数值的取值范围. ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______. 、…、
、…、 、
、 可一般表示为
可一般表示为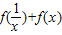 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题: ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.