题目内容
已知函数 的定义域为R,解关于x的不等式x2-x-a2+a>0.
的定义域为R,解关于x的不等式x2-x-a2+a>0.
解:因为函数 的定义域为R,所以ax2+2ax+1≥0恒成立.(*)…(2分)
的定义域为R,所以ax2+2ax+1≥0恒成立.(*)…(2分)
当a=0时,1≥0恒成立,满足题意,…(3分)
当a≠0时,为满足(*)必有a>0且△=4a2-4a≤0,解得0<a≤1,
综上可知:a的取值范围是0≤a≤1.…(6分)
原不等式可化为(x-a)[x-(1-a)]>0,
当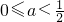 时,不等式的解为:x<a,或x>1-a.…(8分)
时,不等式的解为:x<a,或x>1-a.…(8分)
当 时,不等式的解为:
时,不等式的解为: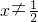 .…(9分)
.…(9分)
当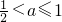 时,不等式的解为:x<1-a,或x>a.…(11分)
时,不等式的解为:x<1-a,或x>a.…(11分)
综上,当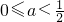 时,不等式的解集为:{x|x<a,或x>1-a};
时,不等式的解集为:{x|x<a,或x>1-a};
当 时,不等式的解集为:
时,不等式的解集为: ;
;
当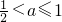 时,不等式的解集为:{x|x<1-a或x>a }.…(12分)
时,不等式的解集为:{x|x<1-a或x>a }.…(12分)
分析:由条件可得0≤a≤1,原不等式可化为(x-a)[x-(1-a)]>0,分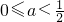 、
、 、
、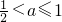 三种情况,分别求出不等式的解集.
三种情况,分别求出不等式的解集.
点评:本题主要考查二元一次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.
 的定义域为R,所以ax2+2ax+1≥0恒成立.(*)…(2分)
的定义域为R,所以ax2+2ax+1≥0恒成立.(*)…(2分)当a=0时,1≥0恒成立,满足题意,…(3分)
当a≠0时,为满足(*)必有a>0且△=4a2-4a≤0,解得0<a≤1,
综上可知:a的取值范围是0≤a≤1.…(6分)
原不等式可化为(x-a)[x-(1-a)]>0,
当
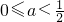 时,不等式的解为:x<a,或x>1-a.…(8分)
时,不等式的解为:x<a,或x>1-a.…(8分)当
 时,不等式的解为:
时,不等式的解为: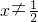 .…(9分)
.…(9分)当
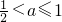 时,不等式的解为:x<1-a,或x>a.…(11分)
时,不等式的解为:x<1-a,或x>a.…(11分)综上,当
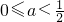 时,不等式的解集为:{x|x<a,或x>1-a};
时,不等式的解集为:{x|x<a,或x>1-a};当
 时,不等式的解集为:
时,不等式的解集为: ;
;当
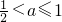 时,不等式的解集为:{x|x<1-a或x>a }.…(12分)
时,不等式的解集为:{x|x<1-a或x>a }.…(12分)分析:由条件可得0≤a≤1,原不等式可化为(x-a)[x-(1-a)]>0,分
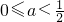 、
、 、
、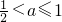 三种情况,分别求出不等式的解集.
三种情况,分别求出不等式的解集.点评:本题主要考查二元一次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 的定义域为R,且当
的定义域为R,且当 时,
时, 恒成立,
恒成立, 对称;
对称; 图象的一个对称点。
图象的一个对称点。 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且
 N*),则
N*),则 的值为( )
的值为( ) 的定义域为R,它的反函数为
的定义域为R,它的反函数为 ,如果
,如果 与
与 互为反函数,且
互为反函数,且 ,则
,则 的值为(
)
的值为(
) B、0
C、
B、0
C、 D、
D、
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且 (
( N*),则
N*),则 的值为( )
的值为( )