题目内容
给定圆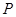 :
: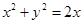 及抛物线
及抛物线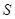 :
: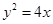 ,过圆心
,过圆心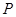 作直线
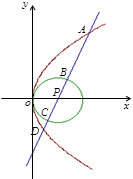
作直线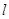 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为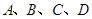 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线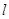 的方程.
的方程.
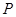 :
: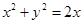 及抛物线
及抛物线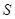 :
: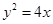 ,过圆心
,过圆心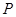 作直线
作直线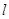 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为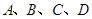 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线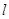 的方程.
的方程.
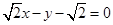 或
或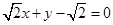 .
.试题分析:本题考查圆、直线、抛物线相交的问题,考查学生分析问题解决问题的能力.先将圆的直径求出来,再设出直线方程,方程中的中有一个参数
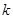 ,本题的关键是解出
,本题的关键是解出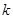 的值,将直线方程代入抛物线方程中,消去
的值,将直线方程代入抛物线方程中,消去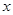 ,求
,求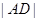 的长,再利用等差中项列出线段
的长,再利用等差中项列出线段 的关系,进而求出
的关系,进而求出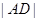 的长,与上面的
的长,与上面的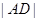 联立就可求出
联立就可求出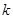 .
.试题解析:圆
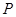 的方程为
的方程为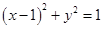 ,则其直径长
,则其直径长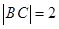 ,圆心为
,圆心为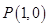 ,设
,设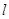 的方程为
的方程为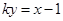 ,即
,即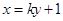 ,代入抛物线方程得:
,代入抛物线方程得: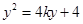 ,设
,设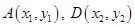 ,有
,有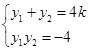 ,
, 则
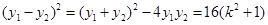 .
. 故
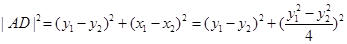
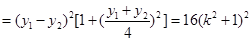 ,
, 因此
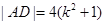 . 8分
. 8分据等差,
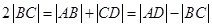 ,
, 所以
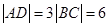 ,即
,即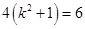 ,
,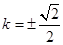 , 14分
, 14分即:
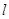 方程为
方程为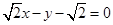 或
或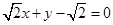 . 16分
. 16分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
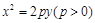 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是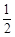 时,
时,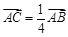 .
.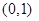 ,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.
,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.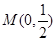 的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为
的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为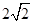 时,求直线m的方程.
时,求直线m的方程.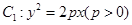 的焦点
的焦点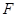 以及椭圆
以及椭圆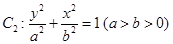 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆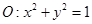 上.
上.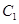 和椭圆
和椭圆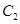 的标准方程;
的标准方程;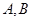 两不同点,交
两不同点,交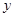 轴于点
轴于点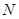 ,已知
,已知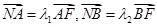 ,求
,求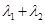 的值;
的值;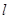 交椭圆
交椭圆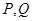 两不同点,
两不同点,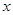 轴的射影分别为
轴的射影分别为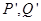 ,
,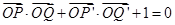 ,若点
,若点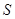 满足
满足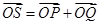 ,证明:点
,证明:点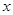 轴,焦点在直线
轴,焦点在直线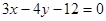 上,则该抛物线的方程为__________.
上,则该抛物线的方程为__________.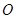 为坐标原点,
为坐标原点,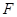 为抛物线
为抛物线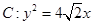 的焦点,
的焦点,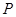 为
为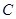 上一点,若
上一点,若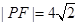 ,则
,则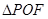 的面积为( )
的面积为( )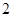
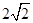
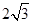
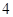
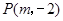 到焦点的距离为4,则
到焦点的距离为4,则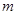 的值为( )
的值为( )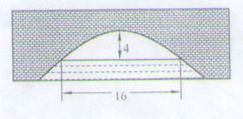
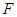 为抛物线
为抛物线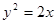 的焦点,
的焦点,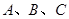 为抛物线上三点,若
为抛物线上三点,若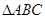 的重心,则
的重心,则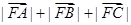 的值为( )
的值为( )