题目内容
设函数f(x)=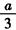
x3+bx2+cx+d(a＞0)，且方程f′（x）-9x=0的两个根分别为1，4，
(Ⅰ)当a=3且曲线y=f(x)过原点时，求f(x)的解析式；
(Ⅱ)若f(x)在（-∞，+∞）内无极值点，求a的取值范围．
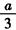x3+bx2+cx+d(a＞0)，且方程f′（x）-9x=0的两个根分别为1，4，(Ⅰ)当a=3且曲线y=f(x)过原点时，求f(x)的解析式；
(Ⅱ)若f(x)在（-∞，+∞）内无极值点，求a的取值范围．
解：由f(x)=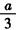
x3+bx2+cx+d得f′(x)=ax2+2bx+c，
因为f′(x)-9x=ax2+2bx+c-9x=0的两个根分别为1，4，
所以，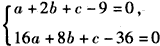
，（*）
(Ⅰ)当a=3时，由(*)式得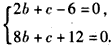
，
解得b=-3，c=12，
又因为曲线y=f(x)过原点，所以d=0，
故f(x)=x3-3x2+12x．
(Ⅱ)由于a＞0，所以“f(x)=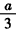
x3+bx2+cx+d在（-∞，+∞）内无极值点”等价于“f'(x)=ax2+2bx+c≥0在（-∞，+∞）内恒成立”，
由（*）式得2b=9-5a，c=4a，
又Δ=(2b)2-4ac=9(a-1)(a-9)，
解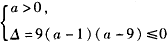
得
，
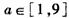即a的取值范围是[1，9]．
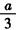x3+bx2+cx+d得f′(x)=ax2+2bx+c，因为f′(x)-9x=ax2+2bx+c-9x=0的两个根分别为1，4，
所以，
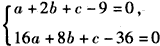，（*）(Ⅰ)当a=3时，由(*)式得
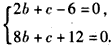，解得b=-3，c=12，
又因为曲线y=f(x)过原点，所以d=0，
故f(x)=x3-3x2+12x．
(Ⅱ)由于a＞0，所以“f(x)=
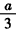x3+bx2+cx+d在（-∞，+∞）内无极值点”等价于“f'(x)=ax2+2bx+c≥0在（-∞，+∞）内恒成立”，由（*）式得2b=9-5a，c=4a，
又Δ=(2b)2-4ac=9(a-1)(a-9)，
解
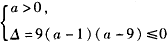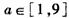得，即a的取值范围是[1，9]．
练习册系列答案
阅读快车系列答案
相关题目
设函数f(x)=x3-(
)x-2，则其零点所在区间为（ ）
| 1 |
| 2 |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |