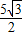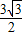题目内容
过点M(2,0)作圆x2+y2=1的两条切线MA,MB(A,B为切点),则
•
=( )
| MA |
| MB |
分析:根据直角三角形中的边角关系,求得MA、MB的值以及∠AMO=∠BMO的值,再利用 两个向量的数量积的定义求得
•
的值.
| MA |
| MB |
解答:解:由圆的切线性质可得,OA⊥MA,OB⊥MB.
直角三角形OAM、OBM中,由sin∠AMO=sin∠BMO=
=
,可得∠AMO=∠BMO=
,
MA=MB=
=
=
,
∴
•
=
×
×cos
=
,
故选D.
直角三角形OAM、OBM中,由sin∠AMO=sin∠BMO=
| r |
| OM |
| 1 |
| 2 |
| π |
| 6 |
MA=MB=
| OM2-r2 |
| 4-1 |
| 3 |
∴
| MA |
| MB |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
| 2 |
故选D.
点评:本题主要考查直角三角形中的边角关系,两个向量的数量积的定义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.
如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.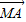 •
•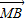 =( )
=( )