题目内容
已知函数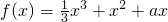 .
.
(1)讨论f(x)的单调性;
(2)设f(x)有两个极值点x1,x2,若过两点(x1,f(x1)),(x2,f(x2))的直线l与x轴的交点在曲线y=f(x)上,求a的值.
解:(1)f′(x)=x2+2x+a=(x+1)2+a-1.
①当a≥1时,f′(x)≥0,
且仅当a=1,x=-1时,f′(x)=0,
所以f(x)是R上的增函数;
②当a<1时,f′(x)=0,有两个根,
x1=-1-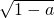 ,x2=-1+
,x2=-1+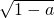 ,
,
当x∈ 时,f′(x)>0,f(x)是增函数.
时,f′(x)>0,f(x)是增函数.
当x∈ 时,f′(x)<0,f(x)是减函数.
时,f′(x)<0,f(x)是减函数.
当x∈ 时,f′(x)>0,f(x)是增函数.
时,f′(x)>0,f(x)是增函数.
(2)由题意x1,x2,是方程f′(x)=0的两个根,
故有a<1, ,
, ,
,
因此 =
=
=
= =
= ,
,
同理 .
.
因此直线l的方程为:y= .
.
设l与x轴的交点为(x0,0)得x0= ,
,

= ,
,
由题设知,点(x0,0)在曲线y=f(x)上,故f(x0)=0,
解得a=0,或a= 或a=
或a=
分析:(1)先对函数进行求导,通过a的取值,求出函数的根,然后通过导函数的值的符号,推出函数的单调性.
(2)根据导函数的根,判断a的范围,进而解出直线l的方程,利用l与x轴的交点为(x0,0),可解出a的值.
点评:本题主要考查函数在某点取得极值的条件,考查分类讨论,函数与方程的思想,考查计算能力.
①当a≥1时,f′(x)≥0,
且仅当a=1,x=-1时,f′(x)=0,
所以f(x)是R上的增函数;
②当a<1时,f′(x)=0,有两个根,
x1=-1-
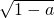 ,x2=-1+
,x2=-1+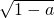 ,
,当x∈
 时,f′(x)>0,f(x)是增函数.
时,f′(x)>0,f(x)是增函数.当x∈
 时,f′(x)<0,f(x)是减函数.
时,f′(x)<0,f(x)是减函数.当x∈
 时,f′(x)>0,f(x)是增函数.
时,f′(x)>0,f(x)是增函数.(2)由题意x1,x2,是方程f′(x)=0的两个根,
故有a<1,
 ,
, ,
,因此
 =
=
=

=
 =
= ,
,同理
 .
.因此直线l的方程为:y=
 .
.设l与x轴的交点为(x0,0)得x0=
 ,
,
=
 ,
,由题设知,点(x0,0)在曲线y=f(x)上,故f(x0)=0,
解得a=0,或a=
 或a=
或a=
分析:(1)先对函数进行求导,通过a的取值,求出函数的根,然后通过导函数的值的符号,推出函数的单调性.
(2)根据导函数的根,判断a的范围,进而解出直线l的方程,利用l与x轴的交点为(x0,0),可解出a的值.
点评:本题主要考查函数在某点取得极值的条件,考查分类讨论,函数与方程的思想,考查计算能力.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
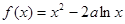 ,
,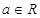
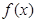 单调区间;
单调区间;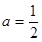 时,证明:当
时,证明:当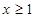 时,证明:
时,证明: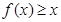 。
。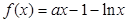
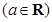 .
.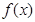 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对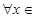
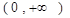 ,
,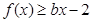 恒成立,求实数
恒成立,求实数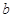 的取值范围.
的取值范围. 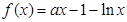
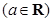 .
.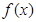 在定义域内的极值点的个数;
在定义域内的极值点的个数;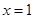 处取得极值,对
处取得极值,对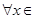
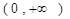 ,
,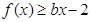 恒成立,求实数
恒成立,求实数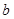 的取值范围;
的取值范围;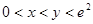 且
且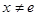 时,试比较
时,试比较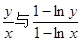 的大小.
的大小. .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列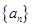 满足
满足 ,求
,求 时,求证:
时,求证: .
. 。(1)讨论函数
。(1)讨论函数 的单调性;(2)当
的单调性;(2)当 时,设
时,设 ,若
,若 时,
时, 恒成立。求整数
恒成立。求整数 的最大值。
的最大值。