题目内容
(本题满分10分)已知曲线 上的动点
上的动点 满足到点
满足到点 的距离比到直线
的距离比到直线  的距离小
的距离小 .
.
(1)求曲线 的方程;
的方程;
(2)动点 在直线
在直线  上,过点
上,过点 作曲线
作曲线 的切线
的切线 ,切点分别为
,切点分别为 、
、 .
.
(ⅰ)求证:直线 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;
(ⅱ)在直线 上是否存在一点
上是否存在一点 ,使得
,使得 为等边三角形(
为等边三角形( 点也在直线
点也在直线 上)?若存在,求出点
上)?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】
.解:(1) 曲线 的方程
的方程  --------------3分
--------------3分
(2)(ⅰ)设
 ,
,

 整理得:
整理得:
同理可得:


又


 --------------------------6分
--------------------------6分
(ⅱ)由(ⅰ)知 中点
中点 ,
,
当 时,则
时,则 的中垂线方程为
的中垂线方程为
 的中垂线与直线
的中垂线与直线 的交点
的交点


若 为等边三角形,则
为等边三角形,则

解得 此时
此时 ,
,
当 时,经检验不存在满足条件的点
时,经检验不存在满足条件的点
综上可得:满足条件的点 存在,坐标为
存在,坐标为 .----------------------10分
.----------------------10分
【解析】略

练习册系列答案
相关题目
 .
.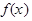 的单调区间;
的单调区间; 且
且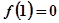 .
. 是偶函数,求函数
是偶函数,求函数 上的最大值和最小值;
上的最大值和最小值; 的取值范围.
的取值范围. ∩
∩ =m,a∥
=m,a∥