题目内容
ABCD是空间四边形,已知AB=CD,AD=BC,但AB≠AD,M,N为两对角线的中点,则( )A.MN与AC,BD都不垂直 B.MN与AC,BD不都垂直
C.MN与AC,BD都垂直 D.无法判定
解析:如图所示,AB=CD,AD=BC,BD公共,
∴△ABD≌△CDB.又M,N为BD,AC的中点,
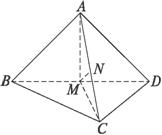
故AM=CM.∴MN⊥AC.
同理,△ADC≌△CBA.
∴BN=DN.
∴MN⊥BD.故C正确.
答案:C
练习册系列答案
相关题目
题目内容
ABCD是空间四边形,已知AB=CD,AD=BC,但AB≠AD,M,N为两对角线的中点,则( )A.MN与AC,BD都不垂直 B.MN与AC,BD不都垂直
C.MN与AC,BD都垂直 D.无法判定
解析:如图所示,AB=CD,AD=BC,BD公共,
∴△ABD≌△CDB.又M,N为BD,AC的中点,
故AM=CM.∴MN⊥AC.
同理,△ADC≌△CBA.
∴BN=DN.
∴MN⊥BD.故C正确.
答案:C
已知ABCD是空间四边形，AB=AD，CB=CD．E为BD的中点．求证：BD⊥平面ACE．
已知四边形ABCD是空间四边形，E，F，G，H分别是边AB，BC，CD，DA的中点，求证：四边形EFGH是平行四边形．