Question

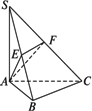
如图所示，SA⊥平面ABC，AB⊥BC，过A作SB的垂线，垂足为E，过E作SC的垂线，垂足为F．

求证：AF⊥SC．

Answer 1

答案：
解析：

分析：本题所要证的是线线垂直，可通过线面垂直来判定，而已知条件为线线垂直、线面垂直，通常我们需要将线面垂直转化为线线垂直，再由线线垂直转化为线面垂直，从而得证． 　　证明： 　　∵SA⊥面ABC，∴SA⊥BC． 　　∵AB⊥BC，∴BC⊥面SAB． 　　∵AE面SAB，∴BC⊥AE． 　　∵AE⊥SB，∴AE⊥面SBC． 　　∴AE⊥SC．又∵EF⊥SC， 　　∴SC⊥面AEF．∴SC⊥AF．

提示：

从已知条件及已有定理入手，直接推证，线线垂直与线面垂直相互转化来加以证明．