题目内容
已知函数f（x）=x2-ax+2在[2，+∞）上单调递增，则实数a的取值范围是（ ）
| A．（-∞，2] | B．[2，+∞） | C．（-∞，4] | D．[4，+∞） |
函数f（x）=x2-ax+2的图象是开口朝上，且以直线x=
为对称轴的抛物线
若函数f（x）=x2-ax+2在[2，+∞）上单调递增，
则
≤2
解得a≤4
故实数a的取值范围是（-∞，4]
故选：C
| a |
| 2 |
若函数f（x）=x2-ax+2在[2，+∞）上单调递增，
则
| a |
| 2 |
解得a≤4
故实数a的取值范围是（-∞，4]
故选：C
练习册系列答案
相关题目
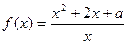
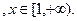若对任意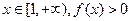
恒成立,试求实数
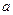的取值范围。
