题目内容
【题目】若有穷数列![]() (
(![]() 是正整数),满足
是正整数),满足![]() 即
即![]() (
(![]() 是正整数,且
是正整数,且![]() ),就称该数列为“对称数列”。例如,数列
),就称该数列为“对称数列”。例如,数列![]() 与数列
与数列![]() 都是“对称数列”.
都是“对称数列”.
(1)已知数列![]() 是项数为9的对称数列,且
是项数为9的对称数列,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列, ![]() ,
, ![]() ,试求
,试求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并求前9项和
,并求前9项和![]() .
.
(2)若![]() 是项数为
是项数为![]() 的对称数列,且
的对称数列,且![]() 构成首项为31,公差为
构成首项为31,公差为![]() 的等差数列,数列
的等差数列,数列![]() 前
前![]() 项和为
项和为![]() ,则当
,则当![]() 为何值时,
为何值时, ![]() 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求![]() 前
前![]() 项的和
项的和![]()
![]() .
.
【答案】(1)见解析(2)当![]() 时,
时, ![]() 取得最大值.
取得最大值. ![]() 的最大值为481.(3)
的最大值为481.(3)![]()
【解析】试题分析:
(1)由数列新定义的知识结合题意可得![]() =11,
=11, ![]() =8,
=8, ![]() ,
, ![]() ,且
,且![]() =66
=66
(2)利用前n项和公式结合二次函数的性质可得当![]() 时,
时, ![]() 取得最大值.
取得最大值. ![]() 的最大值为481.
的最大值为481.
(3)结合通项公式分类讨论可得![]() 前
前![]() 项的和
项的和![]() .
.
试题解析:
解:(1)设![]() 前5项的公差为
前5项的公差为![]() ,则
,则![]() ,解得
,解得 ![]() ,
,
∴![]() =11,
=11, ![]() 2+2×3=8,
2+2×3=8, ![]() ,
, ![]()
∴![]() =2(2+5+8+11+14)-14=66
=2(2+5+8+11+14)-14=66
(2)![]()
![]()
∴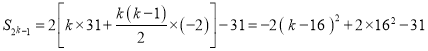
![]() 当
当![]() 时,
时, ![]() 取得最大值.
取得最大值. ![]() 的最大值为481.
的最大值为481.
(3)![]() .
.
由题意得 ![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
当![]() 时,
时, ![]()
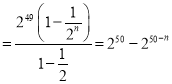 .
.
当![]() 时,
时, ![]()
![]()
![]()
综上所述, ![]()

练习册系列答案
相关题目






