题目内容
已知四面体P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC= AB,若四面体P-ABC的体积为
AB,若四面体P-ABC的体积为 ,则该球的体积为
,则该球的体积为
- A.
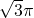
- B.2π
- C.
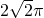
- D.
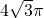
D
分析:设该球的半径为R,则AB=2R,2AC= AB=
AB= ,故AC=
,故AC= R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,由此能求出球的体积.
R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,由此能求出球的体积.
解答:设该球的半径为R,
则AB=2R,2AC= AB=
AB= ,
,
∴AC= R,
R,
由于AB是球的直径,
所以△ABC在大圆所在平面内且有AC⊥BC,
在Rt△ABC中,由勾股定理,得:
BC2=AB2-AC2=R2,
所以Rt△ABC面积S= ×BC×AC=
×BC×AC=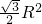 ,
,
又PO⊥平面ABC,且PO=R,四面体P-ABC的体积为 ,
,
∴VP-ABC= =
= ,
,
即 R3=9,R3=3
R3=9,R3=3 ,
,
所以:球的体积V球= ×πR3=
×πR3= ×π×3
×π×3 =4
=4 π.
π.
故选D.
点评:本题考查四面体的外接球的体积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.
分析:设该球的半径为R,则AB=2R,2AC=
 AB=
AB= ,故AC=
,故AC= R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,由此能求出球的体积.
R,由于AB是球的直径,所以△ABC在大圆所在平面内且有AC⊥BC,由此能求出球的体积.解答:设该球的半径为R,
则AB=2R,2AC=
 AB=
AB= ,
,∴AC=
 R,
R,由于AB是球的直径,
所以△ABC在大圆所在平面内且有AC⊥BC,
在Rt△ABC中,由勾股定理,得:
BC2=AB2-AC2=R2,
所以Rt△ABC面积S=
 ×BC×AC=
×BC×AC=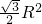 ,
,又PO⊥平面ABC,且PO=R,四面体P-ABC的体积为
 ,
,∴VP-ABC=
 =
= ,
,即
 R3=9,R3=3
R3=9,R3=3 ,
,所以:球的体积V球=
 ×πR3=
×πR3= ×π×3
×π×3 =4
=4 π.
π.故选D.
点评:本题考查四面体的外接球的体积的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
相关题目
已知四面体P-ABC的四个顶点都在球O的球面上,若PB⊥平面ABC,AB⊥AC,且AC=1,PB=AB=2,则球O的表面积为( )
| A、7π | B、8π | C、9π | D、10π |
 如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为
如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为