题目内容
 已知椭圆E:
已知椭圆E: (a>b>0)它的两个焦点为F1(-5
(a>b>0)它的两个焦点为F1(-5 ,0),F2(5
,0),F2(5 ,0),P为椭圆E上一点(点P在第三象限),且△F1 F2的周长等于20+10
,0),P为椭圆E上一点(点P在第三象限),且△F1 F2的周长等于20+10 .
.
(Ⅰ)求椭圆E的方程;
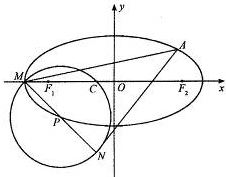
(Ⅱ)若以点P为圆心的圆经过椭圆E的左顶点M与点C(-2,0),直线MP交圆P于另一点N,试在椭圆E上找一点A,使得 取得最小值,并求出最小值.
取得最小值,并求出最小值.
解:(I)由题意可得,|F1F2|=10 =2c,又|PF1|+|PF2|=2a
=2c,又|PF1|+|PF2|=2a
则有2a+2c=20+10
∴a=10
由b2=a2-c2=25
∴椭圆E的标准方程为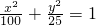
(II)由(I)可得M(-10,0),C(-2,0),设P(m,n),则有m=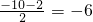
又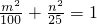
∴n=-4即P(-6,-4)
∵P为MN的中点,可得N(-2,-8),设A(x,y)
∴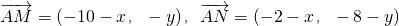
∴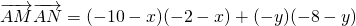
=x2+12x+20+y2+8y
=(x+6)2+(y+4)2-32
当且仅当x=-6,y=-4时,即当A,P重合时,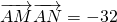 最小
最小
(II)解法二:同(I)可求P(-6,-4),设A(x,y),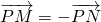
∵ =
=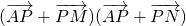
=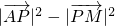 =
=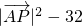
∴当A,P重合时,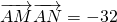 最小
最小
分析:(I)由题意可得,|F1F2|=10 =2c,又|PF1|+|PF2|=2a,结合2a+2c=20+10
=2c,又|PF1|+|PF2|=2a,结合2a+2c=20+10 可求a,c,然后由b2=a2-c2可求b,进而可求椭圆方程
可求a,c,然后由b2=a2-c2可求b,进而可求椭圆方程
(II)法一:由(I)可得M(-10,0),C(-2,0),设P(m,n),则由圆的性质可得m=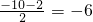 ,结合P在椭圆上可求m,n,即可得P,由题意P为MN的中点,可得N设A(x,y),然后代入
,结合P在椭圆上可求m,n,即可得P,由题意P为MN的中点,可得N设A(x,y),然后代入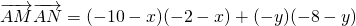 =(x+6)2+(y+4)2-32,可求
=(x+6)2+(y+4)2-32,可求
(II)解法二:同(I)可求P(-6,-4),设A(x,y),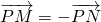 ,代入
,代入 =
=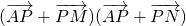 =
=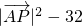 ,可求最小值
,可求最小值
点评:本题考查椭圆的标准方程,以及简单性质的应用,用待定系数法求出椭圆标准方程及向量的数量积的坐标表示是解题的关键.
 =2c,又|PF1|+|PF2|=2a
=2c,又|PF1|+|PF2|=2a则有2a+2c=20+10

∴a=10
由b2=a2-c2=25
∴椭圆E的标准方程为
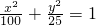
(II)由(I)可得M(-10,0),C(-2,0),设P(m,n),则有m=
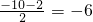
又
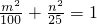
∴n=-4即P(-6,-4)
∵P为MN的中点,可得N(-2,-8),设A(x,y)
∴
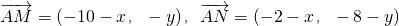
∴
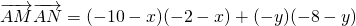
=x2+12x+20+y2+8y
=(x+6)2+(y+4)2-32
当且仅当x=-6,y=-4时,即当A,P重合时,
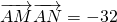 最小
最小(II)解法二:同(I)可求P(-6,-4),设A(x,y),
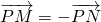
∵
 =
=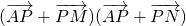
=
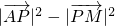 =
=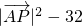
∴当A,P重合时,
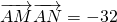 最小
最小分析:(I)由题意可得,|F1F2|=10
 =2c,又|PF1|+|PF2|=2a,结合2a+2c=20+10
=2c,又|PF1|+|PF2|=2a,结合2a+2c=20+10 可求a,c,然后由b2=a2-c2可求b,进而可求椭圆方程
可求a,c,然后由b2=a2-c2可求b,进而可求椭圆方程(II)法一:由(I)可得M(-10,0),C(-2,0),设P(m,n),则由圆的性质可得m=
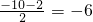 ,结合P在椭圆上可求m,n,即可得P,由题意P为MN的中点,可得N设A(x,y),然后代入
,结合P在椭圆上可求m,n,即可得P,由题意P为MN的中点,可得N设A(x,y),然后代入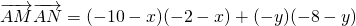 =(x+6)2+(y+4)2-32,可求
=(x+6)2+(y+4)2-32,可求(II)解法二:同(I)可求P(-6,-4),设A(x,y),
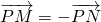 ,代入
,代入 =
=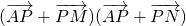 =
=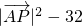 ,可求最小值
,可求最小值点评:本题考查椭圆的标准方程,以及简单性质的应用,用待定系数法求出椭圆标准方程及向量的数量积的坐标表示是解题的关键.

练习册系列答案
相关题目
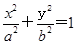 (a>b>0)的离心率e=
(a>b>0)的离心率e=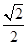 ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2,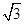 ),点F2在线段PF1的中垂线上
),点F2在线段PF1的中垂线上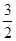 ,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围;
,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围; ,直线l:x+2y-2=0与x轴,y轴分别交于点A,B.
,直线l:x+2y-2=0与x轴,y轴分别交于点A,B. ,A(-a,0),B(0,b),且△ABF的面积为
,A(-a,0),B(0,b),且△ABF的面积为 ,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.
,设斜率为k的直线过点F,且与椭圆E相交于M、N两点. ≤
≤ •
• ≤
≤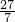 ,求k的取值范围.
,求k的取值范围.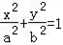 (a>b>0)的右焦点为F(c,0),离心率为
(a>b>0)的右焦点为F(c,0),离心率为 ,A(﹣a,0),
,A(﹣a,0),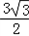 ,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.
,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.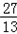 ≤
≤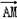 ·
·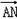 ≤
≤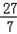 ,求k的取值范围.
,求k的取值范围.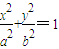 (a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且
(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且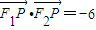 .
.