题目内容
已知椭圆E：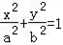
（a＞b＞0）的右焦点为F（c，0），离心率为
，A（﹣a，0），
B（0，b），且△ABF的面积为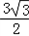
，设斜率为k的直线过点F，且与椭圆E相交于M、N两点．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若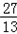
≤
·
≤
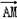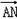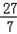，求k的取值范围．
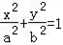（a＞b＞0）的右焦点为F（c，0），离心率为
，A（﹣a，0），B（0，b），且△ABF的面积为
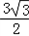，设斜率为k的直线过点F，且与椭圆E相交于M、N两点．（Ⅰ）求椭圆E的方程；
（Ⅱ）若
≤
·
≤
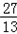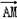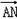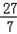，求k的取值范围．解：（Ⅰ）∵离心率为
，
∴a=2c，b=
c．
∵△ABF的面积为
，
∴
，
∴c=1
∴a=2，
∴
∴椭圆E的方程为
；
（Ⅱ）斜率为k的直线过点F，
设方程为y=k（x﹣1）与
联立，
消元可得（3+4k2）x2﹣8k2x+4k2﹣12=0
设M（
，
），N（x2，y2），
则
+x2=
，
∴
y2=k2（
﹣1）（x2﹣1）=
∴
=
x2+2（
+x2）+4+
y2=
∵
≤
≤
，
∴
≤
≤
∴
∴
或
∴k的取值范围是
．
，∴a=2c，b=
c．∵△ABF的面积为
，∴
，∴c=1
∴a=2，
∴
∴椭圆E的方程为
；（Ⅱ）斜率为k的直线过点F，
设方程为y=k（x﹣1）与
联立，消元可得（3+4k2）x2﹣8k2x+4k2﹣12=0
设M（
，
），N（x2，y2），则
+x2=
，
∴
y2=k2（
﹣1）（x2﹣1）=
∴
=
x2+2（
+x2）+4+
y2=
∵
≤
≤
，∴
≤
≤
∴
∴
或
∴k的取值范围是
．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
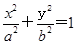（a>b>0）的离心率e＝
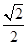，左、右焦点分别为F1、F2，点P（2,
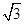），点F2在线段PF1的中垂线上
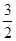，0）且互相垂直的两条直线，l1交E于A， B两点，l2交E于C，D两点，求l1的斜率k的取值范围；
（a＞b＞0）的焦点为F1，F2，离心率为
，直线l：x+2y-2=0与x轴，y轴分别交于点A，B．
，A（-a，0），B（0，b），且△ABF的面积为
，设斜率为k的直线过点F，且与椭圆E相交于M、N两点．
≤
•
≤
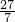，求k的取值范围．
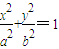（a＞b＞0）过点P（3，1），其左、右焦点分别为F1，F2，且
．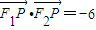