题目内容
(2012•芜湖二模)已知
=(sinx,1),
=(cosx,-
),若f(x)=
•(
-
),求:
(1)f(x)的最小正周期及对称轴方程.
(2)f(x)的单调递增区间.
(3)当x∈[0,
]时,函数f(x)的值域.
| a |
| b |
| 1 |
| 2 |
| a |
| a |
| b |
(1)f(x)的最小正周期及对称轴方程.
(2)f(x)的单调递增区间.
(3)当x∈[0,
| π |
| 2 |
分析:先由向量的运算结合三角函数公式化简为f(x)=2-
sin(2x+
),
(1)由公式易求得得周期和对称轴;
(2)转化为函数y=sin(2x+
)的减区间;
(3)由x的范围开始逐步求解范围,可得答案.
| ||
| 2 |
| π |
| 4 |
(1)由公式易求得得周期和对称轴;
(2)转化为函数y=sin(2x+
| π |
| 4 |
(3)由x的范围开始逐步求解范围,可得答案.
解答:解:由题意可得:f(x)=
2-
•
=sin2x+1-(sinxcosx-
)=
+
-
sin2x
=2-
(sin2x+cos2x)=2-
sin(2x+
)…(4分)
(1)由上可知:T=
=π…(5分)
由2x+
=kπ+
解得:对称轴方程为x=
+
(k∈z)…(7分)
(2)f(x)增区间即为sin(2x+
)的减区间,
由2kπ+
≤2x+
≤2kπ+
,解得
f(x)的单调递增区间为[kπ+
,kπ+
π](k∈z)…(10分)
(3)∵0≤x≤
∴
≤2x+
≤
π
∴-
≤sin(2x+
)≤1
∴值域为[2-
,
]…(13分)
| a |
| a |
| b |
| 1 |
| 2 |
| 1-cos2x |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=2-
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
(1)由上可知:T=
| 2π |
| 2 |
由2x+
| π |
| 4 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 8 |
(2)f(x)增区间即为sin(2x+
| π |
| 4 |
由2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
f(x)的单调递增区间为[kπ+
| π |
| 8 |
| 5 |
| 8 |
(3)∵0≤x≤
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5 |
| 4 |
∴-
| ||
| 2 |
| π |
| 4 |
∴值域为[2-
| ||
| 2 |
| 5 |
| 2 |
点评:本题为三角函数和向量的综合应用,熟练利用公式是解决问题的关键,属中档题.

练习册系列答案
相关题目
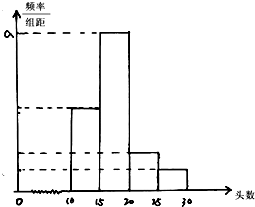 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: