题目内容
16.已知两点A(2,3)与B(4,5),且直线是线段AB的垂直平分线,圆的方程为x2+y2-2x-2y-$\frac{21}{2}$=0,解答下列问题:(1)求直线的方程;
(2)判断直线与圆之间的位置关系,并说明理由.
分析 (1)求出AB的中点坐标为(3,4),AB的斜率为1,可得线段AB的垂直平分线方程;
(2)求出圆心与半径,利用圆心到直线的距离d=r,可得结论.
解答 解:(1)∵两点A(2,3)与B(4,5),
∴AB的中点坐标为(3,4),AB的斜率为1,
∴线段AB的垂直平分线方程为y-4=-(x-3),即x+y-7=0;
(2)圆的方程为x2+y2-2x-2y-$\frac{21}{2}$=0,可化为(x-1)2+(y-1)2=$\frac{25}{2}$,圆心为(1,1),半径为$\frac{5\sqrt{2}}{2}$,
∴圆心到直线的距离d=$\frac{5}{\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$,
∴直线与圆相切.
点评 本题考查直线方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.设等差数列{an}中,a1,a7是方程x2-6x+4=0的两根,则a3+a4+a5=( )
| A. | 4 | B. | 9 | C. | 4或-2 | D. | 4或8 |
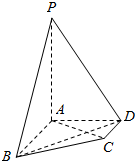 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.