题目内容
已知A,B,C三点不在同一条直线上,O是平面ABC内一定点,P是△ABC内的一
动点,若 ,则直线AP一定过△ABC的( )
,则直线AP一定过△ABC的( )
| A.重心 | B.垂心 | C.外心 | D.内心 |
A
解析试题分析:取BC的中点D,连接AD,因为 ,所以
,所以 ,又λ∈[0,+∞),所以P点在射线AD上,故P的轨迹过△ABC的重心。故选A。
,又λ∈[0,+∞),所以P点在射线AD上,故P的轨迹过△ABC的重心。故选A。
考点:向量的运算;共线向量;三角形的五心。
点评:本题主要考查向量的运算法则、向量共线的充要条件、三角形的重心定义。设出BC的中点D,利用向量的运算法则化简  ,据向量共线的充要条件得到P在三角形的中线上是做此题的关键。三角形的重心定义:三条中线的交点。
,据向量共线的充要条件得到P在三角形的中线上是做此题的关键。三角形的重心定义:三条中线的交点。

练习册系列答案
相关题目
如图,在梯形ABCD中,AD∥BC,则 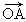 +
+ 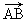 -
- 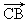 等于( )
等于( )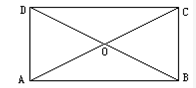
A.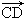 | B.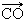 | C.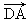 | D. |
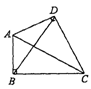
如图,在四边形ABCD中,AB⊥BC,AD⊥DC,.若 则
则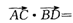 ( )
( )
| A.a2-b2 | B.b2-a2 | C.a2+b2 | D.ab |
平面向量 与
与 的夹角为
的夹角为 ,
, =" 2," |
=" 2," | | = 1,则 |
| = 1,则 | +2
+2 |= ( )
|= ( )
A. | B.2 | C.4 | D.10 |
已知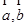 均为单位向量,它们的夹角为60°,那么,
均为单位向量,它们的夹角为60°,那么,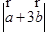 等于( )
等于( )
A. | B.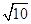 | C.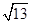 | D.4 |
已知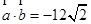 ,
,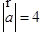 ,
,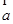 和
和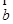 的夹角为
的夹角为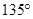 ,则
,则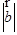 为( )
为( )
A.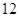 | B.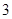 | C.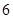 | D.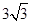 |
已知向量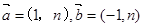 ,若
,若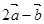 与
与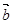 垂直,则
垂直,则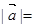 ( )
( )
A.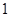 | B.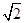 | C.4 | D.2 |
已知平面向量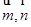 的夹角为
的夹角为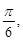 且
且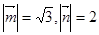 ,在
,在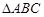 中,
中,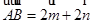 ,
,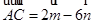 ,
,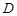 为
为 中点,则
中点,则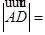 ( )
( )
| A.2 | B.4 | C.6 | D.8 |
若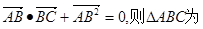 ( )
( )
| A.直角三角形 | B.钝角三角形 |
| C.锐角三角形 | D.等腰三角形 |