题目内容
【题目】已知函数f(x)=(x+a)lnx在x=1处的切线方程为y=x﹣1.
(Ⅰ)求a的值及f(x)的单调区间;
(Ⅱ)记函数y=F(x)的图象为曲线C,设点A(x1 , y1),B(x2 , y2)是曲线C上不同的两点,如果在曲线C上存在点M(x0 , y0),使得①x0= ![]() ;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.试证明:函数f(x)不存在“中值相依切线”.
;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.试证明:函数f(x)不存在“中值相依切线”.
【答案】解:(Ⅰ)由f(x)=(x+a)lnx,得f′(x)=lnx+ ![]() .
.
∴f′(1)=1+a,又f(1)=0,
∴函数f(x)=(x+a)lnx在x=1处的切线方程为y=(1+a)(x﹣1)=(1+a)x﹣1﹣a.
∴1+a=1,得a=0.
则f(x)=xlnx,f′(x)=lnx+1.
由f′(x)=lnx+1=0,得x= ![]() .
.
∴当x∈ ![]() 时,f′(x)<0,当x∈
时,f′(x)<0,当x∈ ![]() 时,f′(x)>0.
时,f′(x)>0.
∴f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增;
上单调递增;
(Ⅱ)假设函数f(x)存在“中值相依切线”.
设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,
则y1=x1lnx1,y2=x2lnx2.
![]() .
.
由f(x)=xlnx的导数为f′(x)=1+lnx,
可得1+ln ![]() =
= ![]() =
= ![]() ,
,
整理得:  ,
,
令 ![]() (t>1),则
(t>1),则 ![]() .
.
令g(t)= ![]() (t>1),
(t>1),
则g′(t)= ![]() ,
,
令h(t)=2t﹣2﹣tlnt﹣lnt,h′(t)=2﹣lnt﹣1﹣ ![]() =1﹣lnt﹣
=1﹣lnt﹣ ![]() ,
,
再令r(t)=1﹣lnt﹣ ![]() ,
,
则r′(t)= ![]() <0,∴r(t)单调递减,
<0,∴r(t)单调递减,
由r(1)=0,∴h′(t)<0,得h(t)单调递减,
又h(1)=0,∴h(t)<0,即g′(t)<0在(1,+∞)上恒成立.
可得g(t)在(1,+∞)上单调递减,则g(t)<g(1)=﹣ln2.
∴ ![]() 不成立,
不成立,
故假设错误,函数f(x)不存在“中值相依切线”.
【解析】(Ⅰ)求出函数f(x)的导函数,得到函数在x=1处的切线方程,结合已知切线方程求得a值,进一步求得函数的单调区间;(Ⅱ)假设函数f(x)存在“中值相依切线”.设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,则y1=x1lnx1,y2=x2lnx2.求出kAB及f′( ![]() ).由题意列等式可得1+ln
).由题意列等式可得1+ln ![]() =
= ![]() =
= ![]() ,整理得:
,整理得:  ,令
,令 ![]() (t>1)换元,则
(t>1)换元,则 ![]() .令g(t)=
.令g(t)= ![]() (t>1),利用导数求得g(t)的最小值小于1﹣ln2,说明计算错误,函数f(x)不存在“中值相依切线”.
(t>1),利用导数求得g(t)的最小值小于1﹣ln2,说明计算错误,函数f(x)不存在“中值相依切线”.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
工种类别 | A | B | C |
赔付频率 | | | |
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.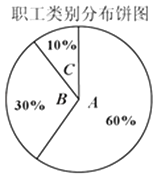
【题目】2016世界特色魅力城市200强新鲜出炉,包括黄山市在内的28个中国城市入选.美丽的黄山风景和人文景观迎来众多宾客.现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 | 30 | ||
女性 | 10 | ||
合计 | 100 |
(1)若在100这人中,按性别分层抽取一个容量为20的样本,女性应抽11人,请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料能否在犯错误的概率不超过0.05前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节游客中随机抽取3人赠送精美纪念品,记这3人中赞成“自助游”人数为X,求X的分布列和数学期望. 附:K2= ![]()
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |