题目内容

4．身穿红、黄两种颜色衣服的各有两人，身穿蓝颜色衣服的有一人，现将这五人排成一行，要求穿相同颜色衣服的人不能相邻，则不同的排法共有（　　）
A．24种B．48种C．36种D．28种

分析 由题意知先使五个人的全排列，共有A55种结果，去掉相同颜色衣服的人相邻的情况，穿红色相邻和穿黄色相邻两种情况，得到结果

解答 解：由题意知先使五个人的全排列，共有A55=120种结果．
穿红色相邻或穿黄色相邻两种情况，有2A22A44=96种，
穿红色相邻且穿黄色也相邻情况，有A22A22A33=24种，
故：穿相同颜色衣服的人不能相邻的排法是120-96+24=48，
故选：B．

点评 本题是一个简单计数问题，在解题时注意应用排除法，从正面来解题时情况比较复杂，所以可以写出所有的结果，再把不合题意的去掉，属于基础题．

练习册系列答案
相关题目
4．若存在x∈[2，3]，使不等式$\frac{1+ax}{x•{2}^{x}}$≥1成立，则实数a的最小值为$\frac{7}{2}$．
5．已知函数f（x）=$\left\{\begin{array}{l}{a{x}^{2}+1，x≥0}\\{（a-1）{e}^{ax}，x＜0}\end{array}\right.$在（-∞，+∞）上是单调函数，则实数a的取值范围是（1，2]．
12．当x＞-1时，函数y=x+$\frac{1}{x+1}$的最小值是1．
19．某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：
①sin213°+cos217°-sin13°cos17°；
②sin215°+cos215°-sin15°cos15°；
③sin218°+cos212°-sin18°cos12°；
④sin2（-18°）+cos248°-sin（-18°）cos48°；
⑤sin2（-25°）+cos255°-sin（-25°）cos55°．
（1）试从上述五个式子中选择一个，求出这个常数；
（2）根据（1）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．
9．如图，该程序运行后输出的结果为是（　　） 
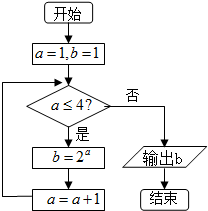
A．2B．4C．8D．16
16．已知xi∈[0，π]，i=1，2，3，…，n，则有
①sinx1=sinx1
②sinx1+sinx2≤2sin$\frac{{{x_1}+{x_2}}}{2}$
③sinx1+sinx2+sinx3≤3sin$\frac{{{x_1}+{x_2}+{x_3}}}{3}$
④sinx1+sinx2+sinx3+sinx4≤4sin$\frac{{{x_1}+{x_2}+{x_3}+{x_4}}}{4}$
由上述结论类比，猜想得到一般的结论是：$sin{x_1}+sin{x_2}+…+sin{x_n}≤nsin\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$．
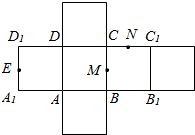13．如图为正方体ABCD-A1B1C1D1的平面展开图，其中E、M、N分别为A1D1、BC、CC1的中点，
（Ⅰ） 作出该正方体的水平放置直观图；
（Ⅱ） 求证：平面BEC1∥平面D1MN．
14．已知两点M（2，0）、N（-2，0），平面上动点P满足|$\overrightarrow{MN}$|•|$\overrightarrow{MP}$|+$\overrightarrow{MN}$•$\overrightarrow{NP}$=0
（1）求动点P的轨迹C的方程．
（2）如果直线x+my+4=0（m∈R）与曲线C交于A、B两点，那么在曲线C上是否存在点D，使得△ABD是以AB为斜边的直角三角形？若存在，求出m的取值范围；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网