题目内容
已知 ,
, .
.
(Ⅰ)求cosA的值;
(Ⅱ)求函数 的值域.
的值域.
解:(Ⅰ)因为 ,且
,且 ,
,
所以 ,
, .
.
因为 =
= .
.
所以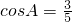 .
.
(Ⅱ)由(Ⅰ)可得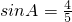 .
.
所以 =1-2sin2x+2sinx=
=1-2sin2x+2sinx= ,x∈R.
,x∈R.
因为sinx∈[-1,1],所以,当 时,f(x)取最大值
时,f(x)取最大值 ;
;
当sinx=-1时,f(x)取最小值-3.
所以函数f(x)的值域为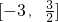 .
.
分析:(Ⅰ)先利用同角三角函数基本关系式求 ,注意对角的范围的判断,再利用两角差的余弦公式将cosA变换为
,注意对角的范围的判断,再利用两角差的余弦公式将cosA变换为 ,代入计算即可
,代入计算即可
(Ⅱ)先将所求函数变换为复合函数f(x)=1-2sin2x+2sinx,再利用三角函数的有界性及配方法求此复合函数的值域即可
点评:本题考察了同角三角函数基本关系式,两角差的余弦公式,通过角变换求三角函数值的技巧,复合函数求值域的方法
 ,且
,且 ,
,所以
 ,
, .
.因为
 =
= .
.所以
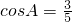 .
. (Ⅱ)由(Ⅰ)可得
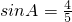 .
.所以
 =1-2sin2x+2sinx=
=1-2sin2x+2sinx= ,x∈R.
,x∈R.因为sinx∈[-1,1],所以,当
 时,f(x)取最大值
时,f(x)取最大值 ;
;当sinx=-1时,f(x)取最小值-3.
所以函数f(x)的值域为
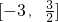 .
.分析:(Ⅰ)先利用同角三角函数基本关系式求
 ,注意对角的范围的判断,再利用两角差的余弦公式将cosA变换为
,注意对角的范围的判断,再利用两角差的余弦公式将cosA变换为 ,代入计算即可
,代入计算即可(Ⅱ)先将所求函数变换为复合函数f(x)=1-2sin2x+2sinx,再利用三角函数的有界性及配方法求此复合函数的值域即可
点评:本题考察了同角三角函数基本关系式,两角差的余弦公式,通过角变换求三角函数值的技巧,复合函数求值域的方法

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,直三棱柱ABC-A′B′C′内接于高为
如图,直三棱柱ABC-A′B′C′内接于高为 (2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c,
(2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c, 已知△OAB是边长为4的正三角形,CO⊥平面OAB,且CO=2,设D、E分别是OA、AB的中点.
已知△OAB是边长为4的正三角形,CO⊥平面OAB,且CO=2,设D、E分别是OA、AB的中点.