题目内容
19．已知抛物线y=x2-4x+1．将此抛物线沿x轴方向向左平移4个单位长度，得到一条新的抛物线．（1）求平移后的抛物线解析式．
（2）若直线y=m与这两条抛物线有且只有四个交点，求实数m的取值范围．
分析 （1）将y=x2-4x+1配方，再由函数图象的平移变换法则，得到平行后的解析式；
（2）求出两条抛物线的顶点坐标和交点坐标，进而可得满足条件的实数m的取值范围．
解答 解：（1）将y=x2-4x+1配方，
得y=（x-2）2-3，向左平移4个单位，
得y=（x+2）2-3，
所以平移后得抛物线的解析式为y=x2+4x+1…（4分）
（2）由（1）可知，两抛物线的顶点坐标为：（2，-3），（-2，-3）．
而又由$\left\{\begin{array}{l}y={x^2}-4x+1\\ y={x^2}+4x+1\end{array}\right.$，解得$\left\{\begin{array}{l}x=0\\ y=1.\end{array}\right.$
所以两条抛物线的交点为（0，1），
如图．由图象知，若直线y=m与两条抛物线有且只有四个交点时，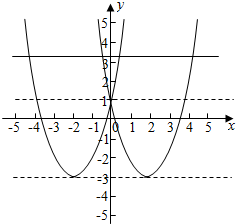
m＞-3且m≠1．…（8分）
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
10．
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜ω）的图象如图所示，为了得到g（x）=Asinωx的图象，可以将f（x）的图象（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜ω）的图象如图所示，为了得到g（x）=Asinωx的图象，可以将f（x）的图象（ ）| A． | 向右平移$\frac{π}{12}$个单位长度 | B． | 向左平移$\frac{π}{12}$个单位长度 | ||
| C． | 向右平移$\frac{π}{6}$个单位长度 | D． | 向左平移$\frac{π}{6}$个单位长度 |
14．函数f（x）=tanωx（ω＞0）的图象的相邻两支截直线$y=\frac{π}{8}$所得线段长为$\frac{π}{8}$，则$f（\frac{π}{8}）$的值是（ ）
| A． | 0 | B． | -1 | C． | 1 | D． | $\frac{π}{8}$ |
4．设函数$f（x）=\left\{\begin{array}{l}1，x为有理数\\-1，x为无理数\end{array}\right.$（ ）
| A． | 函数f（x）的值域为[-1，1] | B． | 函数f（x）在R上为单调函数 | ||
| C． | 函数f（x）为奇函数 | D． | 函数f（x）为偶函数 |