题目内容
(本小题满分l2分)(注意:在试题卷上作答无效)
 如图,四棱锥
如图,四棱锥 中,
中,
 ∥
∥ ,
, ,侧面
,侧面 为等边三角形.
为等边三角形.  .
.
(I) 证明:
(II) 求AB与平面SBC所成角的大小。
【答案】
【分析】第(I)问的证明的突破口是利用等边三角形SAB这个条件,找出AB的中点E,连结SE,DE,就做出了解决这个问题的关键辅助线。
 (II)本题直接找线面角不易找出,要找到与AB平行的其它线进行转移求解。
(II)本题直接找线面角不易找出,要找到与AB平行的其它线进行转移求解。
【命题意图】以四棱锥为载体考查线面垂直证明和线面角的计算,注重与平面几何的综合.
 解法一:(Ⅰ)取
解法一:(Ⅰ)取 中点
中点 ,连结
,连结 ,则四边形
,则四边形 为矩形,
为矩形, ,连结
,连结 ,则
,则 ,
, .
.
又 ,故
,故 ,
,
所以 为直角. ………………3分
为直角. ………………3分
由 ,
, ,
, ,得
,得 平面
平面 ,所以
,所以 .
.
 与两条相交直线
与两条相交直线 、
、 都垂直.
都垂直.
所以 平面
平面 .
………………6分
.
………………6分
另解:由已知易求得 ,于是
,于是 .可知
.可知 ,同理可得
,同理可得 ,又
,又 .所以
.所以 平面
平面 . ………………6分
. ………………6分
(Ⅱ)由 平面
平面 知,平面
知,平面 平面
平面 .
.
作 ,垂足为
,垂足为 ,则
,则 平面ABCD,
平面ABCD, .
.
作 ,垂足为
,垂足为 ,则
,则 .
.
连结 .则
.则 .
.
又 ,故
,故 平面
平面 ,平面
,平面 平面
平面 .……9分
.……9分
作 ,
, 为垂足,则
为垂足,则 平面
平面 .
.
 ,即
,即 到平面
到平面 的距离为
的距离为 .
.
由于 ,所以
,所以 平面
平面 ,
, 到平面
到平面 的距离
的距离 也为
也为 .
.
设 与平面
与平面 所成的角为
所成的角为 ,则
,则 ,
, .……12分
.……12分
 解法二:以
解法二:以 为原点,射线
为原点,射线 为
为 轴的正半轴,建立如图所示的空间直角坐标系
轴的正半轴,建立如图所示的空间直角坐标系 .
.
设 ,则
,则 、
、 .
.
又设 ,则
,则 .
.
(Ⅰ) ,
,
由 得
得
 ,
,
故 .
.
由 得
得 ,
,
又由 得
得 ,
,
即 ,故
,故 .
………………3分
.
………………3分
于是 ,
,
 .
.
故 ,又
,又 ,
,
所以 平面
平面 .
………………6分
.
………………6分
(Ⅱ)设平面 的法向量
的法向量 ,
,
则 .
.
又 ,
,
故 ………………9分
………………9分
取 得
得 ,又
,又
 .
.
故 与平面
与平面 所成的角为
所成的角为 .
………………12分
.
………………12分

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线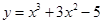 相切的直线方程.
相切的直线方程.