题目内容
如图,在空间直角坐标系中,有长方体ABCD—A′B′C′D′,AB=2,BC=3,AA′=4,求点B到直线A′C的距离.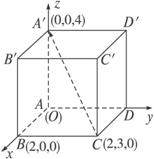
分析:用点到直线的距离公式计算点B到直线A′C的距离d.
解:因为AB=2,BC=3,AA′=4,
所以B(2,0,0),C(2,3,0),A′(0,0,4).
(1)计算直线CA′的方向向量![]() =(0,0,4)-(2,3,0)=(-2,-3,4);
=(0,0,4)-(2,3,0)=(-2,-3,4);
(2)在直线CA′上找到一点C(2,3,0);
(3)![]() =(2,0,0)-(2,3,0)=(0,-3,0);
=(2,0,0)-(2,3,0)=(0,-3,0);
(4)求![]() 在
在![]() 上的投影:
上的投影:
CB·![]() =(0,-3,0)·
=(0,-3,0)·![]()
=(0,-3,0)·(![]() )=0×
)=0×![]() +(-3)×
+(-3)×![]() +0×
+0×![]() =
=![]() ;
;
(5)求点B到直线A′C的距离为
d=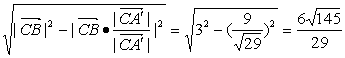 .
.
点拨:求点B到直线CA′的距离的方法和步骤是:
(1)计算直线CA′的方向向量![]() ;(2)找到直线CA′上一点C;(3)求直线CA′上一点C到点B的向量,即
;(2)找到直线CA′上一点C;(3)求直线CA′上一点C到点B的向量,即![]() ;(4)求
;(4)求![]() 在
在![]() 上的投影
上的投影![]() ·
·![]() ;(5)求点B到直线A′C的距离d=
;(5)求点B到直线A′C的距离d=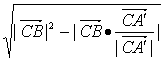 .在求点的坐标、向量的坐标表示、投影及距离时,运算要正确.
.在求点的坐标、向量的坐标表示、投影及距离时,运算要正确.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC, (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
 且
且

