Question

20．已知函数f（x）=sin2x+1．
（1）画出f（x）在x∈[0，π]上的图象；
（2）求f（x）的单调递增区间．

Answer 1

分析 （1）将x的取值，2x的取值及y的取值情况列表，利用五点法作出函数在[0，π]的大致图象即可．
（2）令2kπ-$\frac{π}{2}$≤2x≤2kπ+$\frac{π}{2}$⇒kπ-$\frac{π}{4}$≤x≤kπ+$\frac{π}{4}$．即可解得函数y=sin2x+1的单调递增区间．

解答 解：（1）将x的取值，2x的取值及f（x）的取值情况列表如下：

x	0	$\frac{π}{4}$	$\frac{π}{2}$	$\frac{3π}{4}$	π
2x	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
sin2x+1	1	2	1	0	1

作图如下：

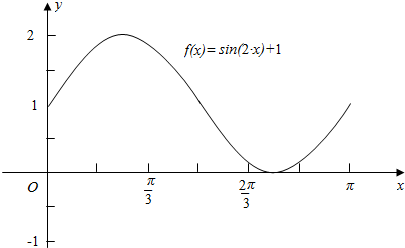
（2）令  2kπ-$\frac{π}{2}$≤2x≤2kπ+$\frac{π}{2}$⇒kπ-$\frac{π}{4}$≤x≤kπ+$\frac{π}{4}$．
∴函数y=sin2x+1的单调递增区间：[kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$]，k∈Z．

点评 本题考查三角函数的单调性，以及函数的图象的作法，解题的关键是熟练掌握正弦函数的性质，作三角函数函数的图象一般用五点法作图，属于基础题．