题目内容
设函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)最高点D的坐标为(2,3).由最高点运动到相邻的最低点时,函数曲线与x轴的交点为(6,0).
(1)求A,ω和φ的值;
(2)求出该函数单调增区间.
(1)求A,ω和φ的值;
(2)求出该函数单调增区间.
分析:(1)函数的最高点D的坐标为(2,3).可得常数A、由最高点运动到相邻的最低点时,函数曲线与x轴的交点为(6,0)求出T,利用周期公式求出ω,利用函数经过(2,3)求出φ.
(2)利用正弦函数的单调增区间,直接求出函数的单调增区间即可.
(2)利用正弦函数的单调增区间,直接求出函数的单调增区间即可.
解答:解:(1)函数的最高点D的坐标为(2,3).可得常数A=3、由最高点运动到相邻的最低点时,函数曲线与x轴的交点为(6,0),所以T=16,由周期公式可得ω=
,函数经过(2,3),3=3sin(
×2+φ),|φ|<π,φ=
.
所以A=3,ω=
,φ=
.
(2)由(1)可知函数y=3sin(
x+
),
因为
x+
∈[2kπ-
,2kπ+
],所以x∈[16k-6,16k],k∈Z.
所以函数的单调增区间为:[16k-6,16k],k∈Z.
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
所以A=3,ω=
| π |
| 8 |
| π |
| 4 |
(2)由(1)可知函数y=3sin(
| π |
| 8 |
| π |
| 4 |
因为
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
所以函数的单调增区间为:[16k-6,16k],k∈Z.
点评:本题是中档题,考查三角函数图象的应用,考查学生的分析问题解决问题的能力,计算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
设函数y=Asin( )(A>0,ω>0),在
)(A>0,ω>0),在 时取最大值A,x=
时取最大值A,x= 时,取最小值-A,则x=π时,函数y的值
时,取最小值-A,则x=π时,函数y的值
[ ]
|
A.仅与ω有关 |
B.仅与 |
C.等于零 |
D.与ω、 |
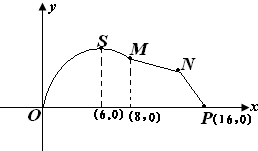 如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4
如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4 有关
有关