题目内容

函数y=(n∈N+，y≠1)的最小值为an，最大值为bn，且cn=4(anbn-)，数列{cn}的前n项和为Sn.

(Ⅰ)求数列{cn}的通项公式；

(Ⅱ)若数列{dn}是等差数列，且dn=，求非零常数c；

(Ⅲ)若f(n)=(n∈N+)，求数列{f(n)}的最大项．

解：(Ⅰ)由y=，(n∈N*，y≠1)，得

x2(y-1)+x+y-n=0 

∵x∈R，y≠1，∴△=1-4(y-1)(y-n)≥0，

即4y2-4(1+n)y+4n-1≤0 

由题意知:an,bn是方程4y2-4(1+n)y+4n-1=0的两根，

∴an·bn=n-，

∴cn=4n-3，(n∈N*)

(Ⅱ) Sn=2n2-n，dn=，

∴d1=，d2=，d3=

∵{dn}为等差数列，∴2d2=d1+d3，∴2c2+c=0，

∴c=或c=0(舍)(

经检验c=时，{dn}为等差数列，dn=2n

(Ⅲ)f(n)==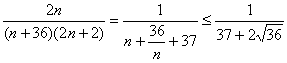

当且仅当n=即n=6时取等号，∴f(n)的最大值为为.

练习册系列答案
相关题目
已知函数y=f（x）的图象经过坐标原点，且f′（x）=2x-1，数列{an}的前n项和Sn=f（n）（n∈N*）．
（I）求数列{an}的通项公式；
（II）若数列{bn}满足an+log3n=log3bn，求数列{bn}的前n项和．
（Ⅲ）设Pn=a1+a4+a7+…+a3n-2，Qn=a10+a12+a14+…+a2n+8，其中n∈N*，试比较Pn与Qn的大小，并证明你的结论．
设定义在R上的函数f（x）=a0x4+a1x3+a2x2+a3x+a4，a0，a1，a2，a3，a4∈R，当x=-1时，f（x）取得极大值
2
3
，且函数y=f（x+1）的图象关于点（-1，0）对称．
（Ⅰ）求f（x）的表达式；
（Ⅱ）在函数y=f（x）的图象上是否存在两点，使以这两点为切点的切线互相垂直，且切点的横坐标都在[-
2
，
2
]上？如果存在，求出点的坐标；如果不存在，请说明理由；
（Ⅲ）设xn=
2n-1
2n
，  ym=
2
(1-3m)
3m
(m，n∈N*)，求证：|f(xn)-f(ym)|＜
4
3
．
已知正项数列{an}中a1=2，点(
an
，an+1)在函数f(x)=
1
3
x3+x的导函数y=f'（x）图象上，数列{bn}中，点（bn，Sn）在直线y=-
1
2
x+3上，其中Sn是数列{bn}的前n项和（n∈N*）
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）若数列{cn}满足cn=
1
2
anbn，且数列{cn}的前n项和Tn，求证：Tn＜
15
4
．
设定义在R上的函数f（x）=ax3+bx2+cx+d（a，b，c，d∈R），当x=-1时f（x）取得极大值
2
3
，且函数y=f（x）为奇函数．
（Ⅰ）求函数f（x）的表达式；
（Ⅱ）设xn=
2n-1
2n
，ym=
2
(1-3m)
3m
(m，n∈N*)，求证：|f(xn)-f(ym)|＜
4
3
．
以下命题正确的是
 
．
①把函数y=3sin(2x+
π
3
)的图象向右平移
π
6
个单位，得到y=3sin2x的图象；
②一平面内两条直线的方程分别是f1（x，y）=0，f2（x，y）=0，它们的交点是P（x0，y0），则方程f1（x，y）+f2（x，y）=0表示的曲线经过点P；
③由“若ab=ac（a≠0，a，b，c，∈R），则b=c”．类比“若
a
•
b
=
a
•
c
(
a
≠
0
，
a
，
b
，
c
为三个向量），则
b
=
c
；
④若等差数列{an}前n项和为sn，则三点(10，
s10
10
)，（100，
s100
100
），（110，
s110
110
）共线．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网