题目内容
设M={y|y=3-x2,x∈R},N={y|y=2x2-1,x∈R},则M∩N=
- A.{y|-3≤y≤13}
- B.{y|-1≤y≤3}
- C.{
 }
} - D.{
 ,-
,- }
}
B
分析:分别求出两集合中两个函数的值域,然后求出两集合的交集即可.
解答:由集合M中的函数y=3-x2≤3,得到集合M={y|y≤3};
由集合N中的函数y=2x2-1≥-1,得到集合N={y|y≥-1},
则M∩N={y|-1≤y≤3}
故选B
点评:此题属于为函数的值域为平台,考查了交集的求法,是一道基础题.
分析:分别求出两集合中两个函数的值域,然后求出两集合的交集即可.
解答:由集合M中的函数y=3-x2≤3,得到集合M={y|y≤3};
由集合N中的函数y=2x2-1≥-1,得到集合N={y|y≥-1},
则M∩N={y|-1≤y≤3}
故选B
点评:此题属于为函数的值域为平台,考查了交集的求法,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设M={y|y=3-x2,x∈R},N={y|y=2x2-1,x∈R},则M∩N=( )
| A、{y|-3≤y≤13} | ||||||||
| B、{y|-1≤y≤3} | ||||||||
C、{
| ||||||||
D、{
|
 }
}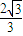 ,-
,-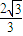 }
}