题目内容
函数f(x)=2acos2x+bsinxcosx满足:f(0)=2,f(
)=
+
.(1)求函数f(x)的最大值和最小值;
(2)若α、β∈(0,π),f(α)=f(β),且α≠β,求tan(α+β)的值.
解:(1)由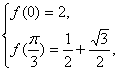得2
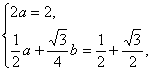
解得a=1,b=2,
∴f(x)=sin2x+cos2x+1=2sin(2x+)+1.
∵-1≤sin(2x+
)≤1,
∴f(x)max=
+1,f(x)min=1-
.
(2)由f(α)=f(β),得sin(2α+
)=sin(2β+
).
∵2α+
、2β+
∈(
,
),且α≠β,
∴2α+
=π-(2β+
)或2α+
=3π-(2β+
),
∴α+β=
或α+β=
,
故tan(α+β)=1.
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知函数f(x)=
，（a＞0），x∈（0，b），则下列判断正确的是（ ）
| a+x2 |
| x |
A、当b＞
| ||||
B、当0＜b≤
| ||||
C、当0＜b≤
| ||||
D、对任意的b＞0，f（x）的最小值均为2
|
选考题
已知二次函数f（x）=ax2+bx+c的图象与x轴有两个交点，且与 x轴、y轴的交点都在负半轴上（如图），则一定有（ ）