题目内容
设函数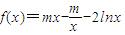 .
.(1)当m=1,x>1时,求证:f(x)>0;
(2)若对于
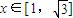 ,均有f(x)<2成立,求实数m的取值范围.
,均有f(x)<2成立,求实数m的取值范围.
【答案】分析:(1)当m=1时,先求出函数的导函数,对?x∈(1,+∞),有f′(x)>0,则f(x)在(1,+∞)为单调增函数,从而f(x)>f(1)=0;
(2)对任意x∈[1, ],则f′(x)<2 恒成立等价于
],则f′(x)<2 恒成立等价于 ,然后讨论m的正负利用导数研究函数在
,然后讨论m的正负利用导数研究函数在 上的最大值即可求出m的范围.
上的最大值即可求出m的范围.
解答:解:(1)当m=1时,f(x)=x- ,
,
对?x∈(1,+∞),有f′(x)>0.∴f(x)在(1,+∞)为单调增函数,∴当x>1时,f(x)>f(1)=0.
(2)对任意x∈[1, ],∴f′(x)<2 恒成立等价于
],∴f′(x)<2 恒成立等价于
当m=0时,∵ ,∴f(x)在[1,
,∴f(x)在[1, ]上为单调减函数.∴f(x)max=f(1)=0<2
]上为单调减函数.∴f(x)max=f(1)=0<2
当m<0时,对任意x∈[1, ],
], ,∴
,∴ 成立.
成立.
当m>0时,
(a)当4-4m2≤0,即m≥1时,f′(x)>0对任意的 恒成立,
恒成立,
∴f(x)在[1, ]上是增函数.∴
]上是增函数.∴ ,
,
由 ,解得
,解得 .∴1≤m<
.∴1≤m< .
.
(b)当4-4m2>0,即0<m<1时,令f′(x)=0,得 ,令
,令 ,得
,得
1)当0<m≤ 时,
时, ,f(x)在[1,
,f(x)在[1, ]上是减函数,∴f(x)max=f(1)=0<2.
]上是减函数,∴f(x)max=f(1)=0<2.
2)当 <m<1时,
<m<1时, ,则f(x)在(1,x2)上是减函数,∴f(x)在
,则f(x)在(1,x2)上是减函数,∴f(x)在 上是增函数,
上是增函数,
∴当x=1或x= 时,f(x)取最大值.∴
时,f(x)取最大值.∴ ,即
,即 ,∴
,∴ <m<1.
<m<1.
综上,m的取值范围是 .
.
点评:本题主要考查了利用导数研究函数单调性和函数的最值,同时考查了函数恒成立问题,是一道综合题,注意分类讨论,计算量比较大.
(2)对任意x∈[1,
 ],则f′(x)<2 恒成立等价于
],则f′(x)<2 恒成立等价于 ,然后讨论m的正负利用导数研究函数在
,然后讨论m的正负利用导数研究函数在 上的最大值即可求出m的范围.
上的最大值即可求出m的范围.解答:解:(1)当m=1时,f(x)=x-
 ,
,
对?x∈(1,+∞),有f′(x)>0.∴f(x)在(1,+∞)为单调增函数,∴当x>1时,f(x)>f(1)=0.
(2)对任意x∈[1,
 ],∴f′(x)<2 恒成立等价于
],∴f′(x)<2 恒成立等价于
当m=0时,∵
 ,∴f(x)在[1,
,∴f(x)在[1, ]上为单调减函数.∴f(x)max=f(1)=0<2
]上为单调减函数.∴f(x)max=f(1)=0<2当m<0时,对任意x∈[1,
 ],
], ,∴
,∴ 成立.
成立.当m>0时,

(a)当4-4m2≤0,即m≥1时,f′(x)>0对任意的
 恒成立,
恒成立,∴f(x)在[1,
 ]上是增函数.∴
]上是增函数.∴ ,
,由
 ,解得
,解得 .∴1≤m<
.∴1≤m< .
.(b)当4-4m2>0,即0<m<1时,令f′(x)=0,得
 ,令
,令 ,得
,得
1)当0<m≤
 时,
时, ,f(x)在[1,
,f(x)在[1, ]上是减函数,∴f(x)max=f(1)=0<2.
]上是减函数,∴f(x)max=f(1)=0<2.2)当
 <m<1时,
<m<1时, ,则f(x)在(1,x2)上是减函数,∴f(x)在
,则f(x)在(1,x2)上是减函数,∴f(x)在 上是增函数,
上是增函数,∴当x=1或x=
 时,f(x)取最大值.∴
时,f(x)取最大值.∴ ,即
,即 ,∴
,∴ <m<1.
<m<1.综上,m的取值范围是
 .
.点评:本题主要考查了利用导数研究函数单调性和函数的最值,同时考查了函数恒成立问题,是一道综合题,注意分类讨论,计算量比较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ,均有f(x)<2成立,求实数m的取值范围.
,均有f(x)<2成立,求实数m的取值范围. .
. 且a3=32,求
且a3=32,求 ;
; .
.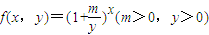 .
.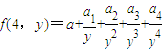 且a3=32,求
且a3=32,求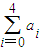 ;
;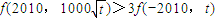 .
.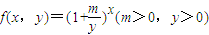 .
.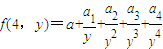 且a3=32,求
且a3=32,求 ;
;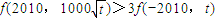 .
.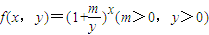 .
.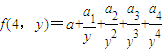 且a3=32,求
且a3=32,求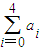 ;
; .
.