题目内容
设函数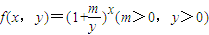 .
.(1)当m=3时,求f(6,y)的展开式中二项式系数最大的项;
(2)若
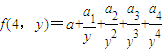 且a3=32,求
且a3=32,求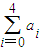 ;
;(3)设n是正整数,t为正实数,实数t满足f(n,1)=mnf(n,t),求证:
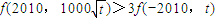 .
.
【答案】分析:(1)利用二项展开式的二项式系数的性质:展开式中中间项的二项式系数最大
(2)利用二项展开式的通项公式求出a3列出方程解得m,通过对y赋值1求出展开式的各项系数和
(3)利用已知等式求出m,t的关系,代入不等式的左边利用二项式的展开式得到左边>3,将m,t的关系代入右边得证.
解答:解:(1)展开式中二项式系数最大的项是第4项= ;
;
(2) ,
,
a3=C43m3=32⇒m=2,
 ;
;
(3)由f(n,1)=mnf(n,t)可得 ,
,
即 ⇒
⇒
 >1+2=3
>1+2=3
而 ,
,
所以 原不等式成立.
原不等式成立.
点评:本题考查二项展开式的二项式系数的性质、二项展开式的通项公式、赋值法求各项系数和、通过二项式的展开式放缩证不等式.
(2)利用二项展开式的通项公式求出a3列出方程解得m,通过对y赋值1求出展开式的各项系数和
(3)利用已知等式求出m,t的关系,代入不等式的左边利用二项式的展开式得到左边>3,将m,t的关系代入右边得证.
解答:解:(1)展开式中二项式系数最大的项是第4项=
 ;
;(2)
 ,
,a3=C43m3=32⇒m=2,
 ;
;(3)由f(n,1)=mnf(n,t)可得
 ,
,即
 ⇒
⇒
 >1+2=3
>1+2=3而
 ,
,所以
 原不等式成立.
原不等式成立.点评:本题考查二项展开式的二项式系数的性质、二项展开式的通项公式、赋值法求各项系数和、通过二项式的展开式放缩证不等式.

练习册系列答案
相关题目
 .
. ,均有f(x)<2成立,求实数m的取值范围.
,均有f(x)<2成立,求实数m的取值范围. .
. 且a3=32,求
且a3=32,求 ;
; .
.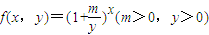 .
.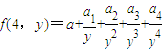 且a3=32,求
且a3=32,求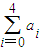 ;
;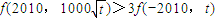 .
.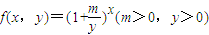 .
.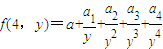 且a3=32,求
且a3=32,求 ;
;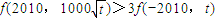 .
.