题目内容
如图,三棱锥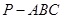 中,
中,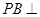 底面
底面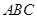 ,
,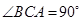 ,
, 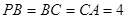 ,
,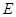 为
为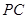 的中点,
的中点,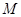 为
为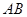 的中点,点
的中点,点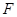 在
在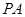 上,且
上,且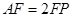 .
.
(1)求证: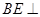 平面
平面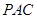 ;
;
(2)求证: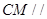 平面
平面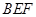 ;
;
(3)求三棱锥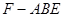 的体积.
的体积.
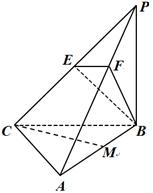
【答案】
(1)证明:∵ 底面
底面 ,且
,且 底面
底面 , ∴
, ∴ …………………1分
…………………1分
由 ,可得
,可得
又
 ,∴
,∴ 平面
平面 …………………………3分
…………………………3分
注意到 平面
平面 , ∴
, ∴ …………………………4分
…………………………4分
 ,
, 为
为 中点,∴
中点,∴ …………………………5分
…………………………5分

 , ∴
, ∴ 平面
平面 …………………………6分
…………………………6分
(2)取 的中点
的中点 ,
, 的中点
的中点 ,连接
,连接 ,
,
∵ 为
为 中点,
中点, ,∴
,∴ .
……………7分
.
……………7分
∵ 平面
平面 平面
平面 , ∴
, ∴ 平面
平面 .
……………8分
.
……………8分
同理可证: 平面
平面 .
.
又 , ∴平面
, ∴平面 平面
平面 . …………9分
. …………9分
∵ 平面
平面 ,∴
,∴ 平面
平面 . …………10分
. …………10分

(3)由(1)可知 平面
平面
又由已知可得 .
.
 …………12分
…………12分
∴
所以三棱锥 的体积为
的体积为 .
…………14分
.
…………14分
【解析】略

练习册系列答案
相关题目
 如图,三棱锥
如图,三棱锥
 中,
中, 底面
底面 ,
, ,
, ,
, 为
为 的中点,点
的中点,点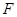 在
在 上,且
上,且 .
.
 平面
平面 ;
;  与平面
与平面 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值. 中,
中, ^底面
^底面 ,若底面
,若底面
 ,若
,若 是
是 的中点,
的中点,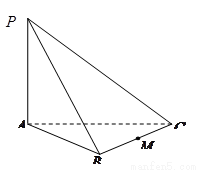
 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).