题目内容
已知函数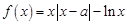 ,
,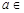
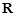 .
.
(Ⅰ)若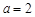 ,求函数
,求函数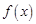 在区间
在区间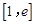 上的最值;
上的最值;
(Ⅱ)若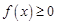 恒成立,求
恒成立,求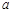 的取值范围. (注:
的取值范围. (注: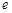 是自然对数的底数)
是自然对数的底数)
【答案】
(Ⅰ) 最大值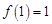 ;(Ⅱ)
;(Ⅱ) 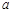 的取值范围是
的取值范围是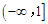 .
.
【解析】
试题分析:(Ⅰ) 讨论去掉绝对值,利用导数求得最值; (Ⅱ) 对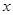 分
分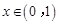 ,
,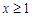 讨论:当
讨论:当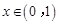 时
时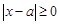 ,
,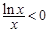 ,
,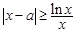 恒成立,所以
恒成立,所以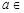
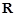 ;当
;当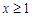 时,对
时,对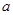 讨论去掉绝对值,分离出
讨论去掉绝对值,分离出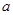 通过求函数的最值求得
通过求函数的最值求得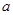 的范围.
的范围.
试题解析:(1) 若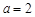 ,则
,则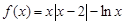 .当
.当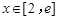 时,
时,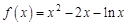 ,
,
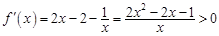 , 所以函数
, 所以函数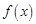 在
在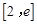 上单调递增;
上单调递增;
当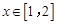 时,
时,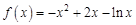 ,
,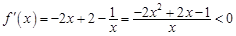 .
.
所以函数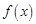 在区间
在区间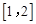 上单调递减,所以
上单调递减,所以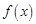 在区间[1,e]上有最小值
在区间[1,e]上有最小值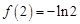 ,又因为
,又因为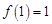 ,
,
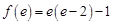 ,而
,而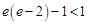 ,所以
,所以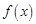 在区间
在区间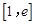 上有最大值
上有最大值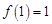 .
.
(2) 函数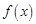 的定义域为
的定义域为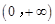 . 由
. 由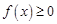 ,得
,得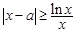 .
(*)
.
(*)
(ⅰ)当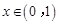 时,
时,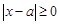 ,
,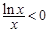 ,不等式(*)恒成立,所以
,不等式(*)恒成立,所以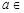
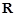 ;
;
(ⅱ)当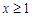 时,
时,
①当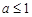 时,由
时,由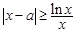 得
得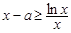 ,即
,即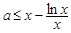 ,
,
现令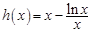 ,
则
,
则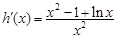 ,因为
,因为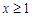 ,所以
,所以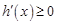 ,故
,故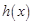 在
在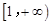 上单调递增,
上单调递增,
从而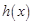 的最小值为
的最小值为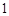 ,因为
,因为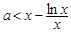 恒成立等价于
恒成立等价于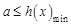 ,所以
,所以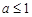 ;
;
②当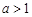 时,
时,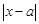 的最小值为
的最小值为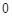 ,而
,而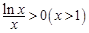 ,显然不满足题意.
,显然不满足题意.
综上可得,满足条件的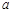 的取值范围是
的取值范围是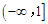 .
.
考点:绝对值的计算、函数的最值求法、利用导数求函数单调性.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|