题目内容
已知某商品生产成本C与产量q的函数关系式为C=100+4q,价格p与产量q的函数关系式为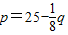 .求产量q为何值时,利润L最大.
.求产量q为何值时,利润L最大.
【答案】分析:首先,设出收入,然后根据价格p与产量q的函数关系式表示出利润的关系式并化简,求导求出单调区间,再根据单调区间判断最值.
解答:解:设收入为R
则:R=q•p=q•(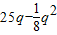 )
)
=25q-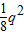
利润L=R-C=(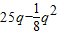 )-(100+4q)
)-(100+4q)
=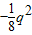 +21q-100 (0<q<200)
+21q-100 (0<q<200)
L'=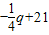
令L'=0
得:q=84
∵0<q<84时
L'>0
当84<q<200时
L'<0
∴当q=84时,L取得最大值,利润最大.
点评:本题考查函数模型的应用,通过对实际问题分析,转化为函数表达式,经过求导求最值,属于基础题.
解答:解:设收入为R
则:R=q•p=q•(
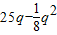 )
)=25q-
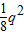
利润L=R-C=(
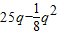 )-(100+4q)
)-(100+4q)=
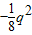 +21q-100 (0<q<200)
+21q-100 (0<q<200)L'=
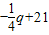
令L'=0
得:q=84
∵0<q<84时
L'>0
当84<q<200时
L'<0
∴当q=84时,L取得最大值,利润最大.
点评:本题考查函数模型的应用,通过对实际问题分析,转化为函数表达式,经过求导求最值,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 .求产量q为何值时,利润L最大?
.求产量q为何值时,利润L最大?