题目内容
已知函数f(x)=asinx+cosx,a∈R;
(Ⅰ)若a=1,求过点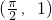 的切线方程;
的切线方程;
(Ⅱ)若a=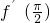 ,求
,求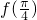 的值.
的值.
解:(Ⅰ)∵a=1,∴f(x)=sinx+cosx,
∴f′(x)=cosx-sinx,
∴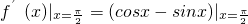 =cos
=cos -sin
-sin =-1,
=-1,
∴过点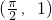 的切线方程为y-1=-(x-
的切线方程为y-1=-(x- ),
),
整理,得x+y-1- =0.
=0.
(Ⅱ)∵f(x)=asinx+cosx,
∴f′(x)=acosx-sinx,
∴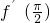 =acos
=acos -sin
-sin =-1,
=-1,
∵a=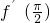 =-1,
=-1,
∴f(x)=-sinx+cosx,
∴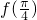 =-sin
=-sin +cos
+cos =-
=- +
+ =0.
=0.
分析:(Ⅰ)由a=1,知f(x)=sinx+cosx,故f′(x)=cosx-sinx,由此及彼能求出函数f(x)上过点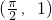 的切线方程.
的切线方程.
(Ⅱ)由f(x)=asinx+cosx,知f′(x)=acosx-sinx,故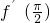 =acos
=acos -sin
-sin =-1,由a=
=-1,由a=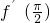 =-1,知f(x)=-sinx+cosx,由此能求出
=-1,知f(x)=-sinx+cosx,由此能求出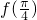 .
.
点评:本题考查函数的切线方程的求法,解题时要认真审题,仔细解答,注意三角函数知识的合理运用.
∴f′(x)=cosx-sinx,
∴
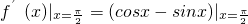 =cos
=cos -sin
-sin =-1,
=-1,∴过点
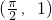 的切线方程为y-1=-(x-
的切线方程为y-1=-(x- ),
),整理,得x+y-1-
 =0.
=0.(Ⅱ)∵f(x)=asinx+cosx,
∴f′(x)=acosx-sinx,
∴
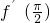 =acos
=acos -sin
-sin =-1,
=-1,∵a=
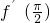 =-1,
=-1,∴f(x)=-sinx+cosx,
∴
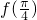 =-sin
=-sin +cos
+cos =-
=- +
+ =0.
=0.分析:(Ⅰ)由a=1,知f(x)=sinx+cosx,故f′(x)=cosx-sinx,由此及彼能求出函数f(x)上过点
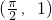 的切线方程.
的切线方程.(Ⅱ)由f(x)=asinx+cosx,知f′(x)=acosx-sinx,故
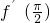 =acos
=acos -sin
-sin =-1,由a=
=-1,由a=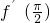 =-1,知f(x)=-sinx+cosx,由此能求出
=-1,知f(x)=-sinx+cosx,由此能求出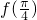 .
.点评:本题考查函数的切线方程的求法,解题时要认真审题,仔细解答,注意三角函数知识的合理运用.

练习册系列答案
相关题目