题目内容
15.已知f(x)是R上的偶函数,当x≥0时,f(x)=$\sqrt{x}$.(1)求f(x)的解析式.
(2)判断f(x)在区间(0,+∞)上的单调性,并证明.
分析 (1)设x<0,则-x>0,将-x代入函数的解析式即可;(2)通过求导判断函数的单调性即可.
解答 解:(1)∵f(x)是R上的偶函数,∴f(-x)=f(x)
当x≥0时,f(x)=$\sqrt{x}$,
设x<0,则-x>0,
∴f(-x)=$\sqrt{-x}$=f(x),
∴f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{\sqrt{-x},x<0}\end{array}\right.$;
(2)函数f(x)在(0,+∞)递增,
证明如下:
由f′(x)=$\frac{1}{2\sqrt{x}}$>0,
得f(x)在(0,+∞)递增.
点评 本题考查了函数的奇偶性和单调性问题,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.函数y=-$\frac{1}{x+1}$在区间[1,2]上的最大值为( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 不存在 |
3.若关于x的方程($\frac{1}{5}$)x=5-a有正根,则( )
| A. | 4<a<5 | B. | a>4 | C. | a<5 | D. | 以上均不对 |
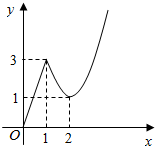 如图,函数f(x)的图象分两段,在[0,1]上为-线段,在[1,+∞)上为抛物线的-段,求f(x)的解析式.
如图,函数f(x)的图象分两段,在[0,1]上为-线段,在[1,+∞)上为抛物线的-段,求f(x)的解析式.