题目内容
设a>1,函数f(x)=log2(x2+2x+a),x∈[-3,3],
(1)求函数f(x)的单调区间;
(2)若f(x)的最大值为5,求f(x)的最小值。
(1)求函数f(x)的单调区间;
(2)若f(x)的最大值为5,求f(x)的最小值。
解:(1)由a>1,知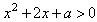 对任意x∈[-3,3]都成立,
对任意x∈[-3,3]都成立,
令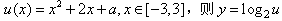 ,
,
且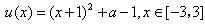 ,
,
∴u(x)在[-3,-1]上为减函数,在[-1,3]上为增函数,
又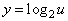 是增函数,
是增函数,
∴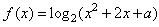 的单调区间为[-3,-1],[-1,3],
的单调区间为[-3,-1],[-1,3],
且f(x)在[-3,-1]上为减函数,在[-1,3]上为增函数;
(2)由(1)的单调性知,f(x)在x=-1处达到最小值,在x=3处达到最大值,
∴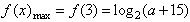 ,
,
依题意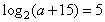 ,解得a=17,
,解得a=17,
∴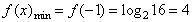 。
。
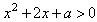 对任意x∈[-3,3]都成立,
对任意x∈[-3,3]都成立,令
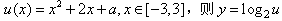 ,
,且
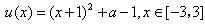 ,
,∴u(x)在[-3,-1]上为减函数,在[-1,3]上为增函数,
又
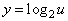 是增函数,
是增函数,∴
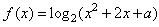 的单调区间为[-3,-1],[-1,3],
的单调区间为[-3,-1],[-1,3],且f(x)在[-3,-1]上为减函数,在[-1,3]上为增函数;
(2)由(1)的单调性知,f(x)在x=-1处达到最小值,在x=3处达到最大值,
∴
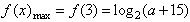 ,
,依题意
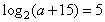 ,解得a=17,
,解得a=17,∴
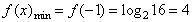 。
。 
练习册系列答案
相关题目