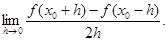题目内容
求下列各极限:(1)
(
-
)；
(2)
［
-x］；
(3)
；
(4)
.
剖析:若f(x)在x0处连续，则应有f(x)=f(x0),故求f(x)在连续点x0处的极限时，只需求f(x0)即可；若f(x)在x0处不连续，可通过变形，消去x-x0因式，转化成可直接求f(x0)的式子.
解:(1)原式===-.
(2)原式==
=a+b,
=
=a+b.
∴原式=a+b.
(3)因为
=1,而
=-1，
≠
,
所以
不存在．
(4)原式=
=
(cos
+sin
)=
.
讲评:(2)中分子、分母应同除以
,所以当x＜0时,应同除以-x.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
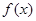在点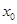
处可导，试求下列各极限的值．
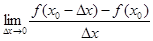；(2)．
[
+
+…+
];
[n(1-
)·(1-
)·…·(1-
)];
[(1+
)·(1+
)·(1+
)·…·(1+
)];
(a≠-3).
