题目内容
（14分）设函数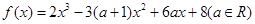
处取得极值
（1）求常数a的值；
（2）求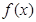
在R上的单调区间；
（3）求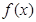在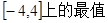
。
【答案】
（1）
因
取得极值， 所以
解得
（3分）
经检验知当
为极值点.
（2分）
（2）由(1)知
故
（5分）
（3）由（2）知
又
（5分）
【解析】略
练习册系列答案
相关题目
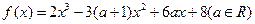
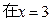处取得极值，求此时函数
的单调区间；
恒成立，求x的取值范围。
处取得极值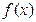
在R上的单调区间；
。
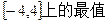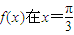处取得极值．
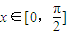恒成立，求b的取值范围；
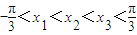，求证：f（sin2A+sin2C）＜f（sin2B）．
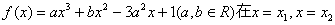处取得极值，且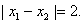
的值，并求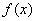
的单调区间；
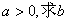的取值范围。