题目内容
f1（x）=sinx，f2（x）=f'1（x），f3（x）=f'2（x），…，fn+1（x）=f'n（x），n∈N+，则f2013（x）=
sinx
sinx
．分析：分别求出前几个函数的导函数，发现导函数以4为周期周期出现，从而可求出f2013（x）的值．
解答：解：f1（x）=sinx，
f2（x）=f'1（x）=cosx，
f3（x）=f'2（x）=-sinx，
f4(x)=f′3(x)=-cosx，
f5(x)=f′4(x)=sinx…
可以看出，以4为周期进行循环
2013=503×4+1
所以f2013（x）=f1（x）=sinx．
故答案为sinx．
f2（x）=f'1（x）=cosx，
f3（x）=f'2（x）=-sinx，
f4(x)=f′3(x)=-cosx，
f5(x)=f′4(x)=sinx…
可以看出，以4为周期进行循环
2013=503×4+1
所以f2013（x）=f1（x）=sinx．
故答案为sinx．
点评：本题考查了导数的运算，考查了基本初等函数的导数公式，解答的关键是通过求解发现规律，是基础题．
练习册系列答案
相关题目
5、已知f1（x）=sinx+cosx，fn+1（x）是fn（x）的导函数，即f2（x）=f1′（x），f3（x）=f2′（x），…，fn+1（x）=fn′（x），n∈N*，则f2011（x）=（ ）
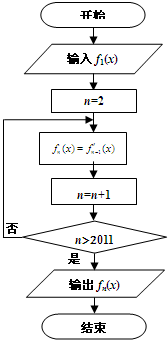在如图所示的程序框图中，当n∈N*（n＞1）时，函数fn（x）表示函数fn-1（x）的导函数，若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）可化为（ ）A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|