题目内容
【题目】已知函数![]() ,且
,且![]() .
.
(1)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1) 函数![]() 在区间
在区间![]() 上是减函数等价于
上是减函数等价于![]() 在区间
在区间![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,由二次函数知识可求
上恒成立,由二次函数知识可求![]() 的范围;
的范围;
(2)令![]() ,当
,当![]() 时,
时,![]() 恒成立等价于
恒成立等价于![]() 在区间
在区间![]() 上恒成立,求函数
上恒成立,求函数![]() 的导数,分类讨论研究函数在区间
的导数,分类讨论研究函数在区间![]() 的单调性求之即可.
的单调性求之即可.
试题解析:(1)∵函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() ,
,
即![]() 在
在![]() 上恒成立,当
上恒成立,当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,①若
,①若![]() ,则
,则![]() ,解得
,解得![]() ;
;
②若![]() ,则
,则![]() ,解得
,解得![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)令![]() ,则
,则![]() ,根据题意,当
,根据题意,当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() .
.
①当![]() 时,
时,![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符题意.
,所以不符题意.
②当![]() 时,
时,![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() 所以不符题意.
所以不符题意.
③当![]() 时,
时,![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,于是“
上是减函数,于是“![]() 对任意
对任意![]() 都成立”的充要条件是
都成立”的充要条件是![]() ,即
,即![]() ,解得
,解得![]() ,故
,故![]() ,综上,
,综上,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表,![]() 的导函数
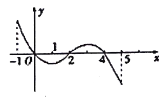
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题:
的命题:
| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
①函数![]() 的极大值点为0,4;
的极大值点为0,4;
②函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
③如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4;
的最大值为4;
④当![]() 时,函数
时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号是__________.