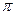题目内容
设函数f（x）=cos（
x+φ）（-π＜φ＜0）．若f（x）+f′（x）是偶函数，则φ=（ ）
| 3 |
A．
| B．-
| C．
| D．-
|
f（x）+f′（x）=cos（
x+φ）-
sin（
x+φ）=2sin（
x+φ+
π），
因为f（x）+f′（x）为偶函数，
所以当x=0时2sin（
x+φ+
π）=±2，则φ+
π=kπ+
，k∈Z，
所以φ=kπ-
，k∈Z，
又-π＜φ＜0，
所以φ=-
．
故选B．
| 3 |
| 3 |
| 3 |
| 3 |
| 5 |
| 6 |
因为f（x）+f′（x）为偶函数，
所以当x=0时2sin（
| 3 |
| 5 |
| 6 |
| 5 |
| 6 |
| π |
| 2 |
所以φ=kπ-
| π |
| 3 |
又-π＜φ＜0，
所以φ=-
| π |
| 3 |
故选B．
练习册系列答案
科学实验活动册系列答案
相关题目
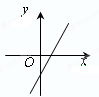
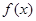的图象如图所示，则不等式
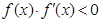的解集为( )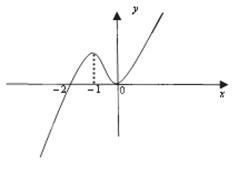
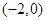
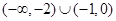
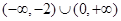
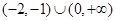
定义域为R，求实数m的取值范围；(2)给出定理：若函数f (x)在[a，b]上连续，且f (a)·f (b)<0，则函数y＝f (x)在区间(a，b)内有零点，即存在x0∈(a，b)，使f (x0)＝0；运用此定理，试判断当k>1时，函数f (x)在(k，2k)内是否存在零点．
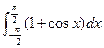等于( )