题目内容

（2009•枣庄一模）不等式
3x-5
x2+2x-3
≤2的解集是（　　）
分析：由不等式
3x-5
x2+2x-3
≤2可得
(2x-1)(x+1)
(x+3)(x-1)
≥0，用穿根法求得它的解集．
解答：解：由不等式
3x-5
x2+2x-3
≤2可得
(2x-1)(x+1)
(x+3)(x-1)
≥0，
用穿根法求得它的解集为
(-∞，-3)∪[-1，
1
2
]∪(1，+∞)，
故选C．
点评：本题主要考查分式不等式的解法，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
（2009•枣庄一模）已知数列{an}的各项均是正数，其前n项和为Sn，满足（p-1）Sn=p2-an，其中p为正常数，且p≠1．
（1）求数列{an}的通项公式；
（2）设bn=
12-logpan
(n∈N*)，求数列{bnbn+1}的前n项和Tn的取值范围；
（3）是否存在正整数M，使得n＞M时，a1a4a7…a3n-2＞a78恒成立？若存在，求出相应的M的最小值；若不存在，请说明理由．
（2009•枣庄一模）设(5x-
1
x
)n的展开式的各项系数和为M，二项式系数和为N，若M-N=240，则展开式中x的系数为（　　）
（2009•枣庄一模）先后抛掷两枚骰子，每次各1枚，求下列事件发生的概率：
（1）事件A：“出现的点数之和大于3”；
（2）事件B：“出现的点数之积是3的倍数”．
（2009•枣庄一模）设复数z的共轭复数是
.
z
，若复数z1=3+4i，z2=t+i，且z1•
.
z2
是实数，则实数t=（　　）
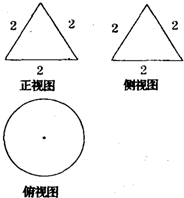（2009•枣庄一模）一个几何体的三视图如图所示，则该几何体外接球的表面积为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网