题目内容
(2009•枣庄一模)已知数列{an}的各项均是正数,其前n项和为Sn,满足(p-1)Sn=p2-an,其中p为正常数,且p≠1.
(1)求数列{an}的通项公式;
(2)设bn=
(n∈N*),求数列{bnbn+1}的前n项和Tn的取值范围;
(3)是否存在正整数M,使得n>M时,a1a4a7…a3n-2>a78恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 | 2-logpan |
(3)是否存在正整数M,使得n>M时,a1a4a7…a3n-2>a78恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由.
分析:(1)利用sn+1-sn=an+1求出an的递推公式,进而求解.
(2)将(1)中的结论代入bn=
,求出bn,进而求出bnbn+1,利用列项法求出Tn,即可求出Tn的范围;
(3)不等式化简可得(
)
>(
)76,讨论p与1的大小,分别求出满足条件的M,从而得到所求.
(2)将(1)中的结论代入bn=
| 1 |
| 2-logpan |
(3)不等式化简可得(
| 1 |
| p |
| n(3n-5) |
| 2 |
| 1 |
| p |
解答:解:(1)由题设知(p-1)a1=p2-a1,解得a1=p.…(1分)
同时
两式作差得(p-1)(Sn+1-Sn)=an-an+1.
所以(p-1)an+1=an-an+1,即an+1=
an,
可见,数列{an}是首项为p,公比为
的等比数列.…(4分)
an=p(
)n-1=(
)n-2.…(5分)
(2)bn=
=
=
.…(7分)
bnbb+1=
=
-
.
Tn=b1b2+b2b3+b3b4+…+bnbn+1=(
-
)+(
-
)+(
-
)+…+(
-
)=1-
…(9分)
所以,Tn∈[
,1)…(10分)
(3)a1a4a7…a3n-2=(
)-1+2+5…(3n-4)=(
)
,
a78=(
)76由题意,要求(
)
>(
)76.…(12分)
①当p>1时,
<76,即3n2-5n-152<0.
解得-
<n<8.不符合题意,此时不存在符合题意的M. …(14分)
②当0<p<1时,
>76,即3n2-5n-152>0.
解得n>8,或n<-
(舍去).此时存在的符合题意的M=8.
综上所述,当0<p<1时,存在M=8符合题意;
当p>1时,不存在正整数M,使得命题成立. …(16分)
同时
|
所以(p-1)an+1=an-an+1,即an+1=
| 1 |
| p |
可见,数列{an}是首项为p,公比为
| 1 |
| p |
an=p(
| 1 |
| p |
| 1 |
| p |
(2)bn=
| 1 |
| 2-logpp2-n |
| 1 |
| 2-(2-n) |
| 1 |
| n |
bnbb+1=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
Tn=b1b2+b2b3+b3b4+…+bnbn+1=(
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
所以,Tn∈[
| 1 |
| 2 |
(3)a1a4a7…a3n-2=(
| 1 |
| p |
| 1 |
| p |
| n(3n-5) |
| 2 |
a78=(
| 1 |
| p |
| 1 |
| p |
| n(3n-5) |
| 2 |
| 1 |
| p |
①当p>1时,
| n(3n-5) |
| 2 |
解得-
| 19 |
| 3 |
②当0<p<1时,
| n(3n-5) |
| 2 |
解得n>8,或n<-
| 19 |
| 3 |
综上所述,当0<p<1时,存在M=8符合题意;
当p>1时,不存在正整数M,使得命题成立. …(16分)
点评:本题主要考查数列知识的综合运用,以及证明不等式的能力,同时考查了裂项求和法,属于中档题.

练习册系列答案
相关题目
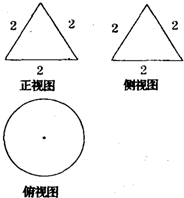 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )