题目内容
函数y=|x-1|+|x-2|+…+|x-20|
- A.图象无对称轴,且在R上不单调
- B.图象无对称轴,且在R上单调递增
- C.图象有对称轴,且在对称轴右侧不单调
- D.图象有对称轴,且在对称轴右侧单调递增
D
分析:函数y=|x-1|+|x-2|+…+|x-20|表示数轴上的x对应点到1,2,3…19,20 对应点的距离之和,分类讨论化简函数的解析式,作出函数的图象,结合图象得出结论.
解答:函数y=|x-1|+|x-2|+…+|x-20|表示数轴上的x对应点到1,2,3…19,20 对应点的距离之和,
当x∈[1,20]时,|x-1|+|x-20|取得最小值等于19,
当x∈[2,19]时,|x-2|+|x-19|取得最小值等于17,
当x∈[3,18]时,|x-3|+|x-18|取得最小值等于15,
…
当x∈[10,11]时,|x-10|+|x-11|取得最小值等于1.
综上,当x∈[10,11]时,函数y=|x-1|+|x-2|+…+|x-20|取得最小值等于19+17+15+…+2+1=100.
当x>20时,函数y=20x-210,
当x<1时,函数y=210-20x,
故函数的图象关于直线 x= 对称,如图所示.
对称,如图所示.
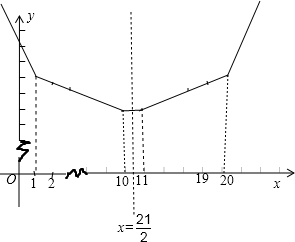
故选 D.
点评:本题主要考查带有绝对值的函数图象的特征,函数的单调性和奇偶性的应用,体现了分类讨论、数形结合的数学思想,属于中档题.
分析:函数y=|x-1|+|x-2|+…+|x-20|表示数轴上的x对应点到1,2,3…19,20 对应点的距离之和,分类讨论化简函数的解析式,作出函数的图象,结合图象得出结论.
解答:函数y=|x-1|+|x-2|+…+|x-20|表示数轴上的x对应点到1,2,3…19,20 对应点的距离之和,
当x∈[1,20]时,|x-1|+|x-20|取得最小值等于19,
当x∈[2,19]时,|x-2|+|x-19|取得最小值等于17,
当x∈[3,18]时,|x-3|+|x-18|取得最小值等于15,
…
当x∈[10,11]时,|x-10|+|x-11|取得最小值等于1.
综上,当x∈[10,11]时,函数y=|x-1|+|x-2|+…+|x-20|取得最小值等于19+17+15+…+2+1=100.
当x>20时,函数y=20x-210,
当x<1时,函数y=210-20x,
故函数的图象关于直线 x=
 对称,如图所示.
对称,如图所示.
故选 D.
点评:本题主要考查带有绝对值的函数图象的特征,函数的单调性和奇偶性的应用,体现了分类讨论、数形结合的数学思想,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
函数y=
+
的定义域是( )
| x-1 |
| 1 |
| lg(2-x) |
| A、(1,2) |
| B、[1,4] |
| C、[1,2) |
| D、(1,2] |
函数y=
的定义域是( )
| x+1 |
| A、(-∞,+∞) |
| B、[-1,+∞) |
| C、[0,+∞] |
| D、(-1,+∞) |