题目内容
为了调查某厂2 000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C
[解析] 根据频率分布直方图可知产品件数在[10,15),[15,20)内的人数分别为5×0.02×20=2,5×0.04×20=4,
设生产产品件数在[10,15)内的2人分别是A,B,设生产产品件数在[15,20)内的4人分别为C,D,E,F,
则从生产低于20件产品的工人中随机地选取2位工人的结果有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种.
2位工人不在同一组的结果有
(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),共8种.
则选取这2人不在同一组的概率为![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
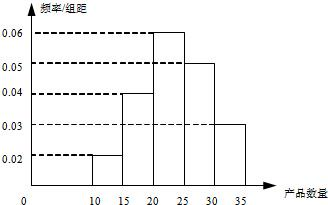 为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位.
为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位. 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
,
 ,
, ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在
 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
, ,
, ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在
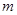 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为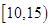 ,
,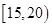 ,
,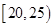 ,
,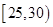 ,
,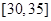 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在