题目内容
14.关于函数f(x)=2cos(2x+$\frac{π}{3}$)的性质,下列表述正确的是(1)、(2)、(4)、(5)(1)是周期函数,且最小正周期是π;
(2)是轴对称图形,且对称轴是直线x=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z;
(3)定义域为R,值域是[$\frac{1}{2}$,2];
(4)是中心对称图形,且对称中心是($\frac{kπ}{2}$+$\frac{π}{12}$,0),k∈Z;
(5)单调递减区间是[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.
分析 由条件利用余弦函数的周期性,定义域和值域,图象的对称性和单调性,逐一判断各个选项是否正确,从而得出结论.
解答 解:对于函数f(x)=2cos(2x+$\frac{π}{3}$),
由于函数的周期为$\frac{2π}{2}$=π,故(1)正确.
令2x+$\frac{π}{3}$=kπ,k∈Z,求得x=$\frac{kπ}{2}$-$\frac{π}{6}$,故函数的图象的对称轴是直线x=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,故(2)正确.
由解析式可得函数的定义域为R,值域为[-2,2],故(3)错误.
令2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,求得x=$\frac{kπ}{2}$+$\frac{π}{12}$,故函数的图象的对称中心为($\frac{kπ}{2}$+$\frac{π}{12}$,0),k∈Z,故(4)正确.
令2kπ≤2x+$\frac{π}{3}$≤2kπ+π,k∈Z,求得 kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,故函数的单调递减区间是[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z,故(5)正确.
故答案为:(1)、(2)、(4)、(5).
点评 本题主要考查余弦函数的周期性,定义域和值域,图象的对称性和单调性,属于基础题.

练习册系列答案
相关题目
9.已知a,b,c,d为实数,满足a+b=c+d=1,ac+bd>1,则在a,b,c,d中( )
| A. | 有且仅有一个为负 | B. | 有且仅有两个为负 | ||
| C. | 至少有一个为负 | D. | 都为正数 |
4.等差数列{an}的前n项和为Sn,如果存在正整数k和l(k≠l),使得Sk=kl2,Sl=lk2,则( )
| A. | Sk+1的最小值为-6 | B. | Sk+l的最大值为-6 | ||
| C. | Sk+1的最小值为6 | D. | Sk+l的最小值为6 |
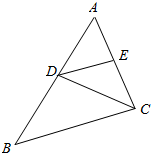
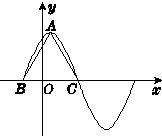 函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.